Cette page est extraitre du tutoriel MFront : tutoriel.pdf.

Comment écrire une loi de comportement: la loi de comportement de Norton

En guise de préliminaire, prenons par exemple la loi de Norton. Elle est définie par: \[\left\{ \begin{aligned} \underline{\epsilon}^{\mathrm{to}}&= \underline{\epsilon}^{\mathrm{el}}+\underline{\epsilon}^{\mathrm{vis}}\\ \underline{\sigma}&= \underline{\mathbf{D}}\,:\,\underline{\epsilon}^{\mathrm{el}}\\ \underline{\dot{\epsilon}}^{\mathrm{vis}}&= \dot{p}\,\underline{n} \\ \dot{p} &= A\,\sigma_{\mathrm{eq}}^{m} \end{aligned} \right.\] où:

• \(\underline{\epsilon}^{\mathrm{to}}\), \(\underline{\epsilon}^{\mathrm{el}}\), \(\underline{\epsilon}^{\mathrm{vis}}\) représentant respectivement les déformations totale, élastique et visqueuse ;
• \(\underline{n}={\displaystyle \frac{\displaystyle 3}{\displaystyle 2}}\,{\displaystyle \frac{\displaystyle \underline{s}}{\displaystyle \sigma_{\mathrm{eq}}}}\) est la direction d’écoulement ;
• \(\underline{s}\) est le déviateur des contraintes ;
• \(\sigma_{\mathrm{eq}}\) est la norme de Von Mises.

L’opérateur d’élasticité \(\underline{\mathbf{D}}\) est calculé à partir du module d’ \(E\) et du coefficient de \(\nu\).

Discrétisation implicite de loi de Norton

Pour intégrer cette loi dans un calcul de structure, il faut procéder à une discrétisation en temps, ce qui revient à définir une suite d’instants de calcul \(\left\{t_{i}\right\}_{1\le i\le I}\).

Pour utiliser un algorithme implicite, il suffit d’écrire toutes les quantités à l’instant \(t_{i}\) et de remplacer les dérivées en temps par leurs incréments sur l’intervalle \(\Delta t= t_{i} - t_{i-1}\) : \[\left\{ \begin{aligned} \Delta\,\underline{\epsilon}^{\mathrm{el}}- \Delta\,\underline{\epsilon}^{\mathrm{to}}+ \Delta\,p\,\underline{n} = 0 \\ \Delta\,p - \Delta\,t\, A\,\sigma_{\mathrm{eq}}^{m} = 0 \end{aligned} \right.\]

avec:

• \(\underline{\sigma}= \underline{\mathbf{D}}\,:\,\underline{\epsilon}^{\mathrm{el}}\) ;
• \(\underline{n}={\displaystyle \frac{\displaystyle 3}{\displaystyle 2}}\,{\displaystyle \frac{\displaystyle \underline{s} \left(t_{i}\right)}{\displaystyle \sigma_{\mathrm{eq}}\left( t_{i}\right)}}\)

On obtient ainsi un système de 7 équations (6 équations — en 3D — relatives à la décomposition additive du tenseur des déformations, et une équation relative à l’écoulement visco-plastique). Les \(7\) inconnues sont les \(6\) composantes de \(\Delta\,\underline{\epsilon}^{\mathrm{el}}\) (en \(3D\)) et \(\Delta p\).

La résolution implicite de ce système est effectuée par une méthode de Newton.

Première implantation

Voici un exemple très simple d’intégration implicite de ce modèle avec MFront :

@Parser Implicit;
@Behaviour Norton;
@Algorithm NewtonRaphson_NumericalJacobian ;

@RequireStiffnessTensor;

@MaterialProperty real A;
@MaterialProperty real m;

@StateVariable real p ;

@ComputeStress{
  sig = D*eel ;
}

@Integrator{
  real seq = sigmaeq(sig) ;
  Stensor n = Stensor(0.) ;
  if(seq > 1.e-12){
    n = 1.5*deviator(sig)/seq ;
  }
  feel += dp*n-deto ;
  fp -= dt*A*pow(seq,m) ;
} // end of @Integrator

@TangentOperator{
  Stensor4 Je ;
  getPartialJacobianInvert(Je) ;
  Dt = D*Je ;
}

Description ligne par ligne

Un fichier commence généralement par une partie déclarative décrivant l’algorithme utilisé pour la résolution, le nom du comportement, puis la liste des propriétés matériau utilisées. On fournit ensuite le nom des variables internes, et la description des équations du système à résoudre.

• la ligne \(1\) précise que nous allons utiliser une méthode d’intégration implicite ;
• la ligne \(2\) donne le nom de la loi ;
• la ligne \(3\) précise que l’on utilise un algorithme avec jacobienne numérique ;
• la ligne \(5\) demande le calcul de la matrice d’élasticité ;
• les lignes \(7\) et \(8\) définissent les propriétés matériau de la loi ;
• la ligne \(10\) déclare la variable interne \(p\). Signalons que la variable interne eel (tenseur déformation élastique \(\underline{\epsilon}^{\mathrm{el}}\)) est prédéfinie par MFront;
• les lignes \(16\) à \(24\) définissent les équations à résoudre ; la convention de nom est la suivante : pour chaque variable interne x, l’incrément est noté dx, et l’équation correspondante fx ;
• la ligne \(17\) demande le calcul de la norme de Von Mises ;
• les lignes \(18\) à \(21\) correspondent au calcul de la direction d’écoulement ;
• la ligne \(22\) définit l’équation \(\Delta\,\underline{\epsilon}^{\mathrm{el}}- \Delta\,\underline{\epsilon}^{\mathrm{to}}+ \Delta\,p\,\underline{n} = 0\). En effet, feel est initialisé à deel et l’opérateur += cumule les valeurs (comme en langage c);
• la ligne \(22\) définit l’équation \(\Delta\, p - \Delta\,t\,A\,\sigma_{\mathrm{eq}}^{m}=0\). Comme précédemment, fp est initialisé à dp, et fp -= xx est équivalent à fp = fp - xx .
• les lignes \(26\) à \(29\) permettent de calculer automatiquement l’opérateur tangent à partir de l’inverse de la matrice jacobienne, comme explicité ci-dessous.

On constate que l’écriture de la loi se limite quasiment à la description des équations. De plus on bénéficie d’un écriture compacte, utilisant des variables tensorielles.

Différentes méthodes d’intégration sont diponibles dans MFront ( [1]). L’algorithme d’intégration utilisé ici (NewtonRaphson\_NumericalJacobian) permet une écriture rapide, et est donc tout à fait adapté au test de modèles.

L’implantation fournit un code beaucoup plus rapide que celle d’un algorithme explicite, mais peut toutefois être optimisée en termes de performances. Pour cela, il suffit d’ajouter les termes de la matrice jacobienne (dérivées des équations par rapport aux inconnues).

De plus, la matrice tangente en sortie de l’intégration est calculée automatiquement à partir de la matrice jacobienne, ce qui permet d’économiser un temps de développement important et conduit à une matrice tangente cohérente de très bonne qualité ([1]). Tout ceci conduit, en très peu de temps, à une intégration robuste, et une convergence très bonne. On voit qu’il est possible de profiter de cette simplicité d’écriture pour effectuer des variantes, des tests de modèles, etc.

MFront gère la compilation de la loi, il suffit de taper dans un terminal :

$ mfront --obuild --interface=aster norton.mfront

ou

$ mfront --obuild --interface=castem norton.mfront

suivant le code que l’on souhaite utiliser. Ceci génère deux répertoires : src et include. Selon l’interface, le répertoire src contient en particulier une bibliothèque dynamique nommée libAsterBehaviour.so pour une exécution avec Code-Aster, ou bien libUmatBehaviour.so pour une exécution avec Cast3M.

Premier test

De plus, l’outil MTest permet d’effectuer très facilement des simulations sur point matériel, permettant de calculer la réponse à des sollicitations en contraintes ou en déformations.

MTest, couplé à un logiciel d’optimisation, permet de plus d’effectuer le recalage des propriétés matériau. Le fichier de données de MTest (nommé ici norton.mtest) se présente de la façon suivante :

@Behaviour<aster> './src/libAsterBehaviour.so' 'asternorton' ;
@MaterialProperty<constant> 'young' 178600.0E6 ;
@MaterialProperty<constant> 'nu' 0.3 ;
@MaterialProperty<constant> 'A' 8.e-67 ;
@MaterialProperty<constant> 'm' 8.2 ;
@ExternalStateVariable 'Temperature' 293.15 ;
@ImposedStress 'SXX' { 0. :  0., 30. : 40.e6};
@ImposedStress 'SXY' { 0. :  0., 30. : 40.e6};
@Times {0.,30. in 100};

• la ligne \(1\) définit la bibliothèque à utiliser et le nom du comportement ;
• les lignes \(2\) à \(5\) définissent les valeurs des propriétés matériau de la loi ;
• la ligne \(6\) déclare la valeur de la température (inutile dans le cas présent) ;
• les lignes \(7\) à \(8\) spécifient le chargement, sous la forme de composantes de contraintes ou de déformations en fonction du temps ;
• la ligne \(9\) définit la discrétisation en temps, donc les instants calculés.

Il suffit alors de lancer le calcul par :

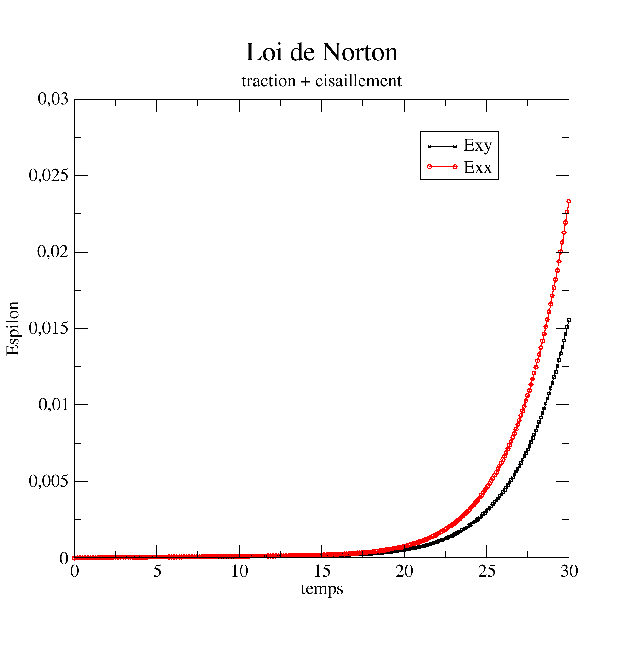
mtest norton.mtest

Ceci produit un fichier résultat norton.res contenant les composantes des tenseurs de déformation, de contrainte, et les variables internes en fonction du temps. La réponse en déformation est représentée ci-dessous:

Références