Next MFront User Day on October 17, 2019 (4/09/2019)

We are pleased to announce that the next MFront User Meeting will be organized by IMSIA (Institute of Mechanical Sciences and Industrial Applications, UMR 9219 CNRS-EDF-CEA-ENSTA).

The User Meeting will be held on October 17 2019 near Paris on the « Plateau of Saclay ». Do not miss this event, which is a great opportunity to communicate with MFront users.

The program of the day is mostly defined (new contributions are still welcomed). Following feedbacks from previous meetings:

• The morning will be dedicated to a general introduction to MFront meant for new users or people willing to have an overview of MFront (beginning at 10h00).
• The afternoon could be dedicated to various technical talks. The following talks are already scheduled (end scheduled at 16h30):
  • New functionalities of TFEL 3.3 (T. Helfer)
  • Modelling non-linear constitutive material laws in FEniCS with MFront (J. Bleyer, Laboratoire Navier)
  • Xper : une plateforme pour la simulation numérique distribuée d’interactions multiphysiques entre corps. (F. Péralès, IRSN)
  • Utilisation de MFront via MGIS dans le code implicite/explicite Mefisto: (O. Jamond, CEA)
  • MFront and OpenGeoSys – connecting two open-source initiatives for simulations in environmental geosciences and energy geotechnics (T. Nagel, Geotechnical Institute)
  • Applications de MFront aux bétons et aux polymères PRFC (Jean-Luc Adia, François Soleilhet EDF R&D)
  • Mfront in biomechanics: Abdominal muscle simulation. (Gerard Fortuny Anguera, Universtitat Rovira i Virgili)

We will made a short introduction to MFront on computers on the morning of October 18 (places will be limited, only a few left) before the “Meeting on Computational Mechanics” at EDF Lab Saclay organized for the 30 years of code_aster.

Access to the user meeting is free but, to facilitate the organization of this event, registration is required. Please register at tfel-contact@cea.fr.

While registering, let us know if you would like to present your work and/or if you would like attend to the first part of the meeting and/or to the second part and/or if you would be interested by the introduction on October 18.

New FEniCS tour of elastoplasticity using the MFront code generator (24/01/2019)

Du to Jeremy Bleyer a new tutorial on how to use MFront with FEniCS in pure python is available: https://comet-fenics.readthedocs.io/en/latest/demo/plasticity_mfront/plasticity_mfront.py.html

This is based on the MGIS (MFrontGenericInterfaceSupport) python bindings (and not the FEniCS bindings which are only available in C++ and currently quite limited), which makes it very easy to use and extend.

You can now use any small strain behaviours written in MFront. Extension to finite strain behaviours is underway and shall be soon available. This development will also help testing the extension of MFront to generalised behaviours,able to cope with higher order mechanical theories (Cosserat medium for instance) and/or multi-physics problems.

TFEL is available as a spack package (27/11/2018)

One easy way to install TFEL under LiNuX and MacOs is to use the spack package manager.

The spack package manager is fully described here: https://spack.readthedocs.io/en/latest/index.html

The following instructions will build the latest development versions:

$ git clone --single-branch -b develop https://github.com/spack/spack.git 
$ . spack/share/spack/setup-env.sh
$ spack install tfel@master

The TFEL package can then be loaded as follows:

$ spack load tfel@master

One nifty feature of spack is that you can install various versions of TFEL in parallel.

Introducing the MFrontGenericInterfaceSupport project (11/09/2018)

This project is meant to ease the integration of MFront in various environments, including homebrew solvers (FE, FFT, etc…). Source code can be found here:

https://github.com/thelfer/MFrontGenericInterfaceSupport.git

The project has a permissive licence for it to be used in both commercial or open-source codes.

Bindings for C are already available. Do not hesitate to consider developping bindings for other languages, such as Python, Fortran, Julia, Java, Matlab, GNU Octave, Scilab, etc.

Announcing the fourth MFront User Day (28/06/2018)

We are pleased to announce the fourth MFront User Day that will held at Cadarche on October the 16th of 2018.

This day will give the opportunity for the developers to present the numerous new features of the 3.2 version and for the users to present their works and to make feed-backs.

All the contributions are welcomed, do not hesitate to contact the organizers to present your work.

The agenda and the location will be communicated later.

The event is free and open to all. However, registration is mandatory. Please send the organizers at the following information:

• Full name.
• Company name.

Please register your participation before September 15th 2018 to facilitate the organisation.

Follow the TFEL/MFront project on ResearchGate (28/06/2018)

TFEL/MFront meets a growing success in the academic work. A ResearchGate project has been created to accompagny this rise:

https://www.researchgate.net/project/TFEL-MFront

A seminar introducing TFEL/MFront at Centrale Lille (21/06/2018)

On the 21th of May, we had the chance to make a seminar about TFEL/MFront at [Centrale Lille.

The talk is available here: https://github.com/thelfer/tfel-doc/tree/master/Talks/CentraleLille2018.

A seminar about TFEL/MFront at the ENSMM (7/06/2018)

On the 7th of May, we had the chance to make a seminar about TFEL/MFront at the ENSMM (École nationale supérieure de mécanique et des microtechniques) Besançon in the Departement of Applied Mechanics.

The talk is available here: https://github.com/thelfer/tfel-doc/tree/master/Talks/ENSMM2018.

Release of version 3.1.2 of TFEL/MFront (31/05/2018)

In prevision of the forthcoming release of the Alcyone fuel performance code, TFEL 3.1.2 has been released. This is mostly a bug fix. Thanks to all the users who reported the issues and contributed to the enhancement of TFEL/MFront.

A special focus is made on Ticket #127 that may change the results of badly convergent behaviours using sub-stepping with the Cast3M and Cyrano interfaces.

A detailed version of the release notes is available here.

Castem 2018 is out (25/05/2018)

Cast3M 2018 has been released.

Binary package for Cast3M 2018 and Windows 64 are now available for download: https://sourceforge.net/projects/tfel/files.

See also the example: http://tfel.sourceforge.net/downloads/windows-install-scripts.tar.bz2. The test directory contains an example showing how to use this binary package. Be sure to change the PATH variable to match your installation directories at the beginning of the mfront-Cast3M2018.bat and launch-Cast3M2018.bat files.

New entry in the gallery: perfect plasticity based on the Drucker-Prager yield criterion and a cap (27/05/2018)

The yield surface is combining two surfaces:

• The first surface is based on the Drucker-Prager yield criterion defined as follows: \[ \sigma_{\mathrm{eq}}^{\mathrm{DP}}=q+\tan{\left(\beta\right)}\,p \] where:
  • \(p\) is the hydrostatique pressure: \[ p = {{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}\,{\mathrm{tr}{\left(\underline{\sigma}\right)}} \]
  • \(q\) is the von Mises norm of the stress tensor \(\underline{\sigma}\): \[ q = \sigma_{\mathrm{eq}}= \sqrt{3\,J_{2}} = \sqrt{{{\displaystyle \frac{\displaystyle 3}{\displaystyle 2}}}\,\underline{s}\,\colon\,\underline{s}} \] where \(\underline{s}\) is the deviatoric part of the stress tensor and \(J_{2}\) the second invariant of \(\underline{s}\). The plastic surface is defined using a constant yield stress \(R_{0}^{\mathrm{DP}}\): \[ \sigma_{\mathrm{eq}}^{\mathrm{DP}}-R_{0}^{\mathrm{DP}}=0 \] This surface is a line in the \({\left(p,q\right)}\) plane.
• The second surface forms a so-called cap which closes the first plastic surface. This plastic surface is based on a criterion close the Green one (See [1] and this page for details): \[ \sigma_{\mathrm{eq}}^{c}=\sqrt{{\left(p-p_{a}\right)}^{2}+{\left(R\,q\right)}^{2}} \] Again, the plastic surface is defined using a constant yield stress \(R_{0}^{c}\), as follows: \[ \sigma_{\mathrm{eq}}^{c}-R_{0}^{c}=0 \]
  This surface is an ellipse in the \({\left(p,q\right)}\) plane.

Simulation of deep drawing for a very anisotropic material (23/05/2018)

This video reproduces the work of Yoon et al (See [2]). in Abaqus/Standard and Abaqus/Explicit. The material is described by Barlat’ Yld2004-18p yield function (See [3]), as described here.

A newly published paper “Void Growth and Coalescence in Irradiated Copper Under Deformation.” (21/04/2018)

A new paper using MFront has been published in the Journal of Nuclear Materials ([4]). See https://doi.org/10.1016/j.jnucmat.2018.01.064 for the online version.

A new constitutive law to model the load induced thermal strain (LITS) of concrete materials (11/04/2018)

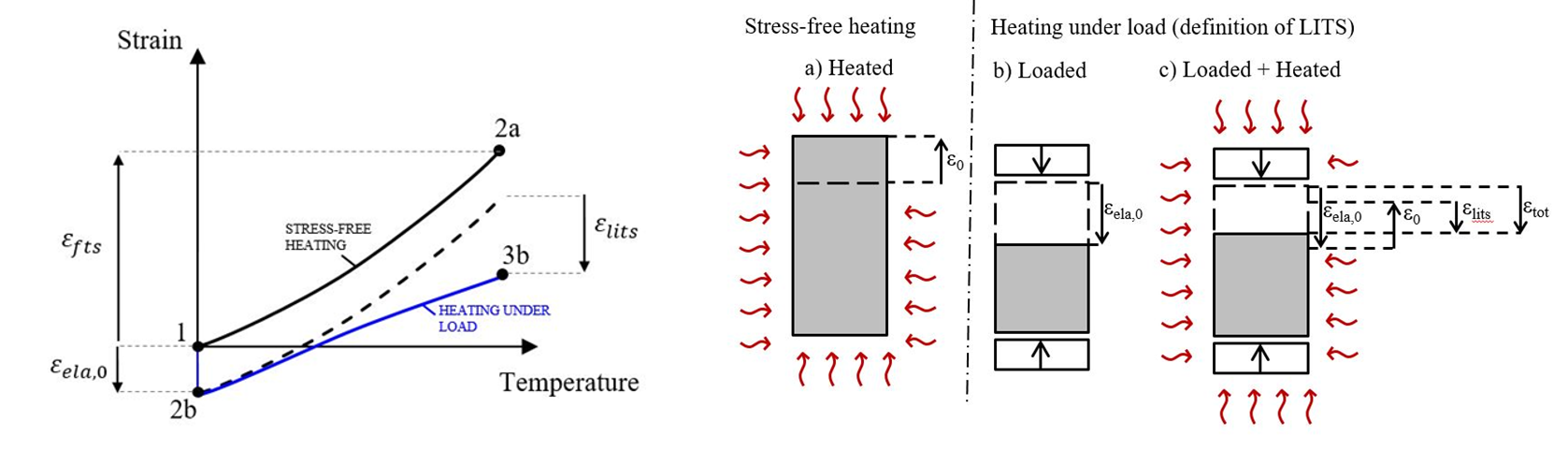
Giacomo Torelli (The University of Cambridge), Parthasarathi Mandal (The University of Manchester) and Martin Gillie (The University of Warwick) developed a new constitutive laws describing the Load-Induced-Thermal-Strain (LITS) which captures the experimentally demonstrated behaviour of concrete in the case of heating under multiaxial mechanical load, for temperatures up to \(500\mbox^{\circ{}}C\).

In contrast to the models available in the literature, this new behaviour takes into account the observed dependency of LITS on stress confinement. Such a dependency is introduced through a confinement coefficient which makes LITS directly proportional to the confinement of the stress state.

Details of theoretical and numerical implementation can be found in [5].

The implementation of the behaviour is available in the MFrontGallery here.

Release of version 3.1.1 of TFEL/MFront (7/03/2017)

In prevision of the 14.2 release of Code_Aster and 2018 release of Salome-Meca, TFEL 3.1.1 has been released. This is mostly a bug fix version with a few enhancements.

A detailed version of the release notes is available here.

Orthotropic generalization of the invariants of the stress deviator tensor (16/11/2018)

Within the framework of the theory of representation, generalizations to orthotropic conditions of the invariants of the deviatoric stress have been proposed by Cazacu and Barlat (see [6]):

• The generalization of \(J_{2}\) is denoted \(J_{2}^{O}\). It is defined by: \[ J_{2}^{O}= a_6\,s_{yz}^2+a_5\,s_{xz}^2+a_4\,s_{xy}^2+\frac{a_2}{6}\,(s_{yy}-s_{zz})^2+\frac{a_3}{6}\,(s_{xx}-s_{zz})^2+\frac{a_1}{6}\,(s_{xx}-s_{yy})^2 \] where the \(\left.a_{i}\right|_{i\in[1:6]}\) are six coefficients describing the orthotropy of the material.
• The generalization of \(J_{3}\) is denoted \(J_{3}^{O}\). It is defined by: \[ \begin{aligned} J_{3}^{O}= &\frac{1}{27}\,(b_1+b_2)\,s_{xx}^3+\frac{1}{27}\,(b_3+b_4)\,s_{yy}^3+\frac{1}{27}\,(2\,(b_1+b_4)-b_2-b_3)\,s_{zz}^3\\ &-\frac{1}{9}\,(b_1\,s_{yy}+b_2s_{zz})\,s_{xx}^2\\ &-\frac{1}{9}\,(b_3\,s_{zz}+b_4\,s_{xx})\,s_{yy}^2\\ &-\frac{1}{9}\,((b_1-b_2+b_4)\,s_{xx}+(b_1-b3+b_4)\,s_{yy})\,s_{zz}^3\\ &+\frac{2}{9}\,(b_1+b_4)\,s_{xx}\,s_{yy}\,s_{zz}\\ &-\frac{s_{xz}^2}{3}\,(2\,b_9\,s_{yy}-b_8\,s_{zz}-(2\,b_9-b_8)\,s_{xx})\\ &-\frac{s_{xy}^2}{3}\,(2\,b_{10}\,s_{zz}-b_5\,s_{yy}-(2\,b_{10}-b_5)\,s_{xx})\\ &-\frac{s_{yz}^2}{3}\,((b_6+b_7)\,s_{xx}-b_6\,s_{yy}-b_7\,s_{zz})\\ &+2\,b_{11}\,s_{xy}\,s_{xz}\,s_{yz} \end{aligned} \] where the \(\left.b_{i}\right|_{i\in[1:11]}\) are eleven coefficients describing the orthotropy of the material.

Those invariants may be used to generalize isotropic yield criteria based on \(J_{2}\) and \(J_{3}\) invariants to orthotropy.

The following functions

\(J_{2}^{0}\), \(J_{3}^{0}\) and their first and second derivatives with respect to the stress tensor \(\underline{\sigma}\) can be computed by the following functions:

• computesJ2O, computesJ2ODerivative and computesJ2OSecondDerivative.
• computesJ3O, computesJ3ODerivative and computesJ3OSecondDerivative.

Those functions take the stress tensor as first argument and each orthotropic coefficients. Each of those functions has an overload taking the stress tensor as its firs arguments and a tiny vector (tfel::math::tvector) containing the orthotropic coefficients.

Efficient computations of the first and second derivatives of the invariants of the stress deviator tensor with respect to the stress (10/01/2018)

Let \(\underline{\sigma}\) be a stress tensor. Its deviatoric part \(\underline{s}\) is:

\[ \underline{s}=\underline{\sigma}-{{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}\,{\mathrm{tr}{\left(\underline{\sigma}\right)}}\,\underline{I} ={\left(\underline{\underline{\mathbf{I}}}-{{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}\,\underline{I}\,\otimes\,\underline{I}\right)}\,\colon\,\underline{\sigma} \]

The deviator of a tensor can be computed using the deviator function.

As it is a second order tensor, the stress deviator tensor also has a set of invariants, which can be obtained using the same procedure used to calculate the invariants of the stress tensor. It can be shown that the principal directions of the stress deviator tensor \(s_{ij}\) are the same as the principal directions of the stress tensor \(\sigma_{ij}\). Thus, the characteristic equation is

\[ \left| s_{ij}- \lambda\delta_{ij} \right| = -\lambda^3+J_1\lambda^2-J_2\lambda+J_3=0, \]

where \(J_1\), \(J_2\) and \(J_3\) are the first, second, and third deviatoric stress invariants, respectively. Their values are the same (invariant) regardless of the orientation of the coordinate system chosen. These deviatoric stress invariants can be expressed as a function of the components of \(s_{ij}\) or its principal values \(s_1\), \(s_2\), and \(s_3\), or alternatively, as a function of \(\sigma_{ij}\) or its principal values \(\sigma_1\), \(\sigma_2\), and \(\sigma_3\). Thus,

\[ \begin{aligned} J_1 &= s_{kk}=0,\, \\ J_2 &= \textstyle{\frac{1}{2}}s_{ij}s_{ji} = {{\displaystyle \frac{\displaystyle 1}{\displaystyle 2}}}{\mathrm{tr}{\left(\underline{s}^2\right)}}\\ &= {{\displaystyle \frac{\displaystyle 1}{\displaystyle 2}}}(s_1^2 + s_2^2 + s_3^2) \\ &= {{\displaystyle \frac{\displaystyle 1}{\displaystyle 6}}}\left[(\sigma_{11} - \sigma_{22})^2 + (\sigma_{22} - \sigma_{33})^2 + (\sigma_{33} - \sigma_{11})^2 \right ] + \sigma_{12}^2 + \sigma_{23}^2 + \sigma_{31}^2 \\ &= {{\displaystyle \frac{\displaystyle 1}{\displaystyle 6}}}\left[(\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_3 - \sigma_1)^2 \right ] \\ &= {{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}I_1^2-I_2 = \frac{1}{2}\left[{\mathrm{tr}{\left(\underline{\sigma}^2\right)}} - \frac{1}{3}{\mathrm{tr}{\left(\underline{\sigma}\right)}}^2\right],\,\\ J_3 &= \det(s_{ij}) \\ &= {{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}s_{ij}s_{jk}s_{ki} = {{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}} {\mathrm{tr}{\left(\underline{s}^3\right)}}\\ &= {{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}(s_1^3 + s_2^3 + s_3^3) \\ &= s_1s_2s_3 \\ &= {{\displaystyle \frac{\displaystyle 2}{\displaystyle 27}}}I_1^3 - {{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}I_1 I_2 + I_3 = {{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}\left[{\mathrm{tr}{\left(\underline{\sigma}^3\right)}} - {\mathrm{tr}{\left(\underline{\sigma}^2\right)}}{\mathrm{tr}{\left(\underline{\sigma}\right)}} +{{\displaystyle \frac{\displaystyle 2}{\displaystyle 9}}}{\mathrm{tr}{\left(\underline{\sigma}\right)}}^3\right]. \end{aligned} \]

where \(I_{1}\), \(I_{2}\) and \(I_{3}\) are the invariants of \(\underline{\sigma}\).

\(J_{2}\) and \(J_{3}\) are building blocks for many isotropic yield critera. Classically, \(J_{2}\) is directly related to the von Mises stress \(\sigma_{\mathrm{eq}}\):

\[ \sigma_{\mathrm{eq}}=\sqrt{{{\displaystyle \frac{\displaystyle 3}{\displaystyle 2}}}\,\underline{s}\,\colon\,\underline{s}}=\sqrt{3\,J_{2}} \]

The first and second derivatives of \(J_{2}\) with respect to \(\sigma\) can be trivially implemented, as follows:

constexpr const auto id  = stensor<N,real>::Id();
constexpr const auto id4 = st2tost2<N,real>::Id();
// first derivative of J2
const auto dJ2  = deviator(sig);
// second derivative of J2
const auto d2J2 = eval(id4-(id^id)/3);

In comparison, the computation of the first and second derivatives of \(J_{3}\) with respect to \(\sigma\) are more cumbersome. In previous versions TFEL, one had to write:

constexpr const auto id = stensor<N,real>::Id();
constexpr const auto id4 = st2tost2<N,real>::Id();
const auto I1   = trace(sig);
const auto I2   = (I1*I1-trace(square(sig)))/2;
const auto dI2  = I1*id-sig;
const auto dI3  = computeDeterminantDerivative(sig);
const auto d2I2 = (id^id)-id4;
const auto d2I3 = computeDeterminantSecondDerivative(sig);
// first derivative of J3
const auto dJ3  = eval((2*I1*I1/9)*id-(I2*id+I1*dI2)/3+dI3);
// second derivative of J3
const auto d2J3 = eval((4*I1/9)*(id^id)-((id^dI2)+(dI2^id)+i1*d2I2)/3+d2I3);

More efficient implementations are now available using the computeDeviatorDeterminantDerivative and computeDeviatorDeterminantSecondDerivative functions:

// first derivative of J3
const auto dJ3  = computeDeviatorDeterminantDerivative(sig);
// second derivative of J3
const auto d2J3 = computeDeviatorDeterminantSecondDerivative(sig);

The doxygen documentation (4/01/2018)

Further documentation for advanced users has been published: the internal code documentation of the project, as generated by doxygen, is now available online:

http://tfel.sourceforge.net/doxygen/index.html

The theme has been adapted from:

https://github.com/Velron/doxygen-bootstrapped

Release of versions 3.1 and 3.0.3 of TFEL/MFront (15/12/2017)

Versions 3.1 and 3.0.3 of TFEL, MFront and MTest has been released on the 15th December, 2017.

Version 3.1

A detailed version of the release notes is available here.

Highlights

From a user point of view, TFEL 3.1 brings many important features:

• The gallery is a list of detailed documentations about implementing clean, efficient and reliable mechanical behaviour using MFront that will be updated as TFEL and MFront evolve. In each case, the integration algorithm is fully described. The gallery currently contains \(17\) entries covering finite strain elasticity, finite strain viscoplasticity, damage, plasticity and viscoplasticity. The gallery. Those implementations are also gathered in a cmake projects called MFrontGallery which can be cloned on github: https://github.com/thelfer/MFrontGallery
• The integration of the TFEL/NUMODIS library which provides many functionalities associated with single crystal description coming from the NUMODIS project. Those functionalities are available in MFront through many new keywords that simplify to a great extent the way small and finite strain single crystal behaviours can be written. See the following page for a detailled description: http://tfel.sourceforge.net/singlecrystal.html
• The DDIF2 behaviour is used in CEA fuel performances codes to describe cracking of the nuclear fuel. The DDIF2 brick allows this model to be easily coupled to the viscplastic behaviour of the fuel material and can be used as easily as the StandardElasticity brick. See this page for details: http://tfel.sourceforge.net/ddif2.html
• An important work has been devoted to enhance the overall numerical reproducibility and stability of the algorithms of TFEL/Math. It is now much safer to use the -ffast-math option in gcc and clang which can drastically increase the efficiency of the generated code. This option is automatically added when using the --obuild=level2 option of mfront. See the release notes for details.
• Support for the Hershey/Hosford yield criteria which generalizes the Mises criteria. Indeed the Hershey/Hosford yield criteria lies between the Mises criteria and the Tresca criteria. Various functions have been introduced to compute the equivalent stress associated with this criteria, its first and second derivatives. See this page for details: http://tfel.sourceforge.net/tensors.html
• Support for the Barlat yield criteria which generalizes the Hill criteria. Various functions have been introduced to compute the equivalent stress associated with this criteria, its first and second derivatives. See this page for details: http://tfel.sourceforge.net/tensors.html
• Abritrary non linear constraints can now be defined in MTest.
• Better support of the Windows platform. Using the cmake generator, using mfront on windows with the Microsoft compilers is easy and closely follows the existing practices on other operating systems.
• Improved installation options. Two versions, or the same version in different flavours (compiled in debug mode, compiled with different compilers), of TFEL/MFront can now be installed in parallel. See http://tfel.sourceforge.net/install.html for details.

Mechanical behaviours

New interfaces

Two new interfaces have been introduced in MFront:

• A native interface for the CalculiX solver. Here native is used to distinguish this interface from the Abaqus/Standard interface which can also be used within CalculiX. This interface can be used with CalculiX 2.13.
• An interface for the ANSYS APDL solver. The latter is still experimental.

The @NumericallyComputedJacobianBlocks keyword

Computing the jacobian of the implicit system is the most difficult part of implementing a behaviour. Computing the jacobian by finite difference is interesting but significantly decreases the performances of the behaviour and can be (very) sensitive to the choice of the numerical perturbation.

The @NumericallyComputedJacobianBlocks keyword is used select a list of jacobian blocks that have to be computed numerically. This is more efficient than computing the whole jacobian numerically. Combined with the ability to compare the jacobian to a numerical approximation, the user now has the ability to build the jacobian incrementally, block by block and checks at each steps that their analytical expressions are correct.

Portability

Portability is a convincing sign of software quality and maintainability:

• usage of functionalities specific to operating systems are well identified.
• it demonstrates that the code is not dependant of the system libraries, such as the C or C++ libraries.

TFEL has been tested successfully on a various flavours of LinuX and BSD systems (including FreeBSD and OpenBSD). The first ones are mostly build on gcc, libstdc++ and the glibc. The second ones are build on clang and libc++.

TFEL can be build on Windows in a wide variety of configurations and compilers:

• native ports can be build using the Visual Studio (2015 and 2017) or MingGW compilers.
• TFEL can be build in the Cygwin environment.

TFEL have reported to build successfully in the Windows Subsystem for LinuX (WSL) environment.

Although not officially supported, more exotic systems, such as OpenSolaris and Haiku, have also been tested successfully. The Minix operating systems provides a pre-release of clang 3.4 that fails to compile TFEL.

Supported compilers

Version 3.1 has been tested using the following compilers:

• gcc on various POSIX systems: versions 4.7, 4.8, 4.9, 5.1, 5.2, 6.1, 6.2, 7.1, 7.2
• clang on various POSIX systems: versions 3.5, 3.6, 3.7, 3.8, 3.9, 4.0, 5.0
• intel. The only tested version is the 2018 version on LinuX. Intel compilers 15 and 16 are known not to work due to a bug in the EDG front-end that can’t parse a syntax mandatory for the expression template engine. The same bug affects the Blitz++ library (see http://dsec.pku.edu.cn/~mendl/blitz/manual/blitz11.html). Version 2017 shall work but were not tested.
• Visual Studio The only supported versions are the 2015 and 2017 versions. Previous versions do not provide a suitable C++11 support.
• PGI compiler (NVIDIA): version 17.10 on LinuX
• MinGW has been tested successfully in a wide variety of configurations/versions, including the version delivered with Cast3M 2017.

Benchmarcks

Concerning the PGI compilers, performances may be affected by the fact that this compiler generates huge shared libraries (three to ten times larger than other compilers).

Version 3.0.3

This is mainly a bug fix version of the 3.0 series. Detailed release notes are available here. There are no known regressions.

New entry in the gallery: perfect plasticity based on the Green yield criterion (30/11/2017)

The Green yield criterion is based on the definition of an equivalent stress \(\sigma_{\mathrm{eq}}\) defined as follows: \[ \sigma_{\mathrm{eq}}=\sqrt{{{\displaystyle \frac{\displaystyle 3}{\displaystyle 2}}}\,C\,\underline{s}\,\colon\,\underline{s}+F\,{\mathrm{tr}{\left(\underline{\sigma}\right)}}^{2}} \] where \(\underline{s}\) is the deviatoric stress tensor: \[ \underline{s}=\underline{\sigma}-{{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}\,{\mathrm{tr}{\left(\underline{\sigma}\right)}}\,\underline{I} \]

A new entry in the gallery shows how to build a perfect plastic behaviour based on this equivalent stress. The implementation is available here: https://github.com/thelfer/MFrontGallery/blob/master/generic-behaviours/plasticity/GreenPerfectPlasticity.mfront

Barlat stress (24/11/2017)

Functions to compute the Barlat equivalent stress and its first and second derivatives are now available in TFEL/Material.

The Barlat equivalent stress is defined as follows (See [3]): \[ \sigma_{\mathrm{eq}}^{B}= \sqrt[a]{ \frac{1}{4}\left( \sum_{i=0}^{3} \sum_{j=0}^{3} {\left|s'_{i}-s''_{j}\right|}^{a} \right) } \]

where \(s'_{i}\) and \(s''_{i}\) are the eigenvalues of two transformed stresses \(\underline{s}'\) and \(\underline{s}''\) by two linear transformation \(\underline{\underline{\mathbf{L}}}'\) and \(\underline{\underline{\mathbf{L}}}''\): \[ \left\{ \begin{aligned} \underline{s}' &= \underline{\underline{\mathbf{L'}}} \,\colon\,\underline{\sigma}\\ \underline{s}'' &= \underline{\underline{\mathbf{L''}}}\,\colon\,\underline{\sigma}\\ \end{aligned} \right. \]

The linear transformations \(\underline{\underline{\mathbf{L}}}'\) and \(\underline{\underline{\mathbf{L}}}''\) are defined by \(9\) coefficients (each) which describe the material orthotropy. There are defined through auxiliary linear transformations \(\underline{\underline{\mathbf{C}}}'\) and \(\underline{\underline{\mathbf{C}}}''\) as follows: \[ \begin{aligned} \underline{\underline{\mathbf{L}}}' &=\underline{\underline{\mathbf{C}}}'\,\colon\,\underline{\underline{\mathbf{M}}} \\ \underline{\underline{\mathbf{L}}}''&=\underline{\underline{\mathbf{C}}}''\,\colon\,\underline{\underline{\mathbf{M}}} \end{aligned} \] where \(\underline{\underline{\mathbf{M}}}\) is the transformation of the stress to its deviator: \[ \underline{\underline{\mathbf{M}}}=\underline{\underline{\mathbf{I}}}-{{\displaystyle \frac{\displaystyle 1}{\displaystyle 3}}}\underline{I}\,\otimes\,\underline{I} \]

The linear transformations \(\underline{\underline{\mathbf{C}}}'\) and \(\underline{\underline{\mathbf{C}}}''\) of the deviator stress are defined as follows: \[ \underline{\underline{\mathbf{C}}}'= \begin{pmatrix} 0 & -c'_{12} & -c'_{13} & 0 & 0 & 0 \\ -c'_{21} & 0 & -c'_{23} & 0 & 0 & 0 \\ -c'_{31} & -c'_{32} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & c'_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & c'_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & c'_{66} \\ \end{pmatrix} \quad \text{and} \quad \underline{\underline{\mathbf{C}}}''= \begin{pmatrix} 0 & -c''_{12} & -c''_{13} & 0 & 0 & 0 \\ -c''_{21} & 0 & -c''_{23} & 0 & 0 & 0 \\ -c''_{31} & -c''_{32} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & c''_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & c''_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & c''_{66} \\ \end{pmatrix} \]

When all the coefficients \(c'_{ji}\) and \(c''_{ji}\) are equal to \(1\), the Barlat equivalent stress reduces to the Hosford equivalent stress.

The following function has been implemented:

• computeBarlatStress: return the Barlat equivalent stress
• computeBarlatStressNormal: return a tuple containg the Barlat equivalent stress and its first derivative (the normal)
• computeBarlatStressSecondDerivative: return a tuple containg the Barlat equivalent stress, its first derivative (the normal) and the second derivative.

The implementation of those functions are greatly inspired by the work of Scherzinger (see [7]). In particular, great care is given to avoid overflows in the computations of the Barlat stress.

Those functions have two template parameters:

• the type of symmetric tensors used for the stress tensor (automatically deduced, but required if the second parameter is specified).
• the eigen solver to be used.

Example

The following example computes the Barlat equivalent stress, its normal and second derivative:

const auto l1 = makeBarlatLinearTransformation<N,double>(-0.069888,0.936408,
                                                         0.079143,1.003060,
                                                         0.524741,1.363180,
                                                         1.023770,1.069060,
                                                         0.954322);
const auto l2 = makeBarlatLinearTransformation<N,double>(-0.981171,0.476741,
                                                         0.575316,0.866827,
                                                         1.145010,-0.079294,
                                                         1.051660,1.147100,
                                                         1.404620);
stress seq;
Stensor  n;
Stensor4 dn;
std::tie(seq,n,dn) = computeBarlatStressSecondDerivative(s,l1,l2,a,seps);

In this example, s is the stress tensor, a is the Hosford exponent, seps is a numerical parameter used to detect when two eigenvalues are equal.

If C++-17 is available, the previous code can be made much more readable:

const auto l1 = makeBarlatLinearTransformation<N,double>(-0.069888,0.936408,
                                                         0.079143,1.003060,
                                                         0.524741,1.363180,
                                                         1.023770,1.069060,
                                                         0.954322);
const auto l2 = makeBarlatLinearTransformation<N,double>(-0.981171,0.476741,
                                                         0.575316,0.866827,
                                                         1.145010,-0.079294,
                                                         1.051660,1.147100,
                                                         1.404620);
const auto [seq,n,dn] = computeBarlatStressSecondDerivative(s,l1,l2,a,seps);

Hosford equivalent stress (17/10/2017)

The header TFEL/Material/Hosford1972YieldCriterion.hxx introduces three functions which are meant to compute the Hosford equivalent stress and its first and second derivatives. This header is automatically included by MFront

The Hosford equivalent stress is defined by: \[ \sigma_{\mathrm{eq}}=\sqrt{{{\displaystyle \frac{\displaystyle 1}{\displaystyle 2}}}{\left({\left|\sigma_{1}-\sigma_{2}\right|}^{2}+{\left|\sigma_{1}-\sigma_{3}\right|}^{2}+{\left|\sigma_{2}-\sigma_{3}\right|}^{2}\right)}} \] where \(s_{1}\), \(s_{2}\) and \(s_{3}\) are the eigenvalues of the stress.

Therefore, when \(a\) goes to infinity, the Hosford stress reduces to the Tresca stress. When \(n = 2\) the Hosford stress reduces to the von Mises stress.

The following function has been implemented:

• computeHosfordStress: return the Hosford equivalent stress
• computeHosfordStressNormal: return a tuple containg the Hosford equivalent stress and its first derivative (the normal)
• computeHosfordStressSecondDerivative: return a tuple containg the Hosford equivalent stress, its first derivative (the normal) and the second derivative.

Example

The following example computes the Hosford equivalent stress, its normal and second derivative:

stress seq;
Stensor  n;
Stensor4 dn;
std::tie(seq,n,dn) = computeHosfordStressSecondDerivative(s,a,seps);

In this example, s is the stress tensor, a is the Hosford exponent, seps is a numerical parameter used to detect when two eigenvalues are equal.

If C++-17 is available, the previous code can be made much more readable:

const auto [seq,n,dn] = computeHosfordStressSecondDerivative(s,a,seps);

Release of TFEL 3.0.2 (25/10/2017)

Version 3.0.2 of TFEL, MFront and MTest has been released on the 25th October, 2017.

This is mainly a bug fix version of the 3.0 series. Detailed release notes are available here. There are no known regressions.

Behaviours for modelling mild steel (14/09/2017)

Thanks to Guillaume Michal, University of Wollongong (NSW, Australia), several implementation of behaviours suitable for the description of mild steel are now available:

• Three versions of the Johnson-Cook behaviour:
  • JohnsonCook_s: which describes strain hardening but does not describe rate effects,
  • JohnsonCook_ssr : which describes both strain hardening and rate effects.
  • JohnsonCook_ssrt: which describes both strain hardening, rate effects and adiabatic heating.
• The Rusinek-Klepaczko law as described in: “Constitutive relations in 3-D for a wide range of strain rates and temperatures - Application to mild steels.” A. Rusinek, R. Zaera and J. R. Klepaczko. Int. J. of Solids and Structures, Vol. 44, 5611-5634, 2007.

Support for the total lagragian framework in Code_Aster

Thanks to M. Abbas, MFront finite strain behaviours can now be used in the total lagragian framework in Code_Aster (called GROT_GDEP). First tests confirm that the robustness and the effiency of this framework are much better than with the SIMO_MIEHE framework.

First tests of MFront in the Windows Subsystem for LinuX environment (3/08/2017)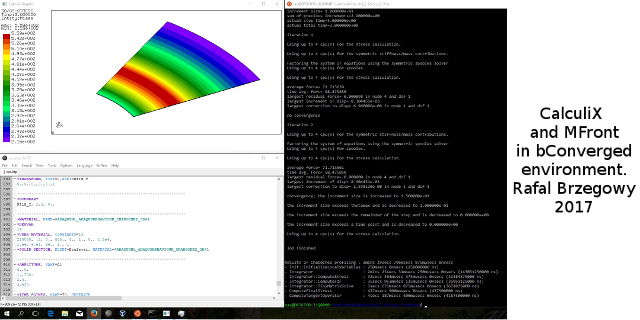

After Visual Studio, Mingw and Cygwin, there is a new way to get MFront working on Windows !

Rafal Brzegowy have successfully compiled and tested MFront using the Windows Subsystem for LinuX (WSL). He was able to use MFront generated behaviours with CalculiX delivered by the bConverged suite.

All tests worked, except some tests related to the long double support in WSL.

Official twitter account (1/08/2017)

TFEL and MFront now have their official twitter account !

We will use it to spread various events and developments make in TFEL and MFront.

A spanish introduction to MFront and Salome-Meca (1/08/2017)

Thanks to Jordi Alberich, a spanish introduction to MFront and Salome-Meca is available here:

http://tfel.sourceforge.net/tutorial-spanish.html

The talks of the third MFront Users Day (21 June 2017)

The talks of the third MFront Users Day are available here:

https://github.com/thelfer/tfel-doc

Cast3m 2017 is out (12 May 2017)

Cast3M 2017 has been released.

A binary version of TFEL compiled for Cast3M 2017 is now available for download on sourceforge:

https://sourceforge.net/projects/tfel/files/

Non linear constraints with MTest

Arbitrary non linear constraints can be now imposed in MTest using @NonLinearConstraint keyword.

Applications

Abritray non linear constraints can be used to:

• Impose a constant stress triaxiality.
• Impose a constant first Piola-Kirchoff stress in a creep test described in finite strain.

On the physical meaning of a constraint

A constraint \(c\) is imposed by introducing a Lagrange multiplier \(\lambda\).

Consider a small strain elastic behaviour characterised by its free energy \(\Psi\). In the only loading is the constraint \(c\), the solution satisfies: \[ \underset{\underline{\varepsilon},\lambda}{\min}\Psi-\lambda\,c \]

In this case, the constraint \(c\) is equivalent to the following imposed stress:

\[ -\lambda\,{\displaystyle \frac{\displaystyle \partial c}{\displaystyle \partial \underline{\varepsilon}}} \]

If the constraint is \(\sigma_{xx}-\sigma_{0}\), where \(\sigma_{0}\) is a constant value, the previous equation shows that imposing this constraint is not equivalent to imposing an uniaxial stress state \(\left(\sigma_{xx}\,0\,0\,0\,0\,0\right)\).

[MFront Gallery] How to implement an isotropic viscoplastic behaviour with several kinematic variables following the Amstrong-Frederic evolution (27/03/2017)

The implementation of an an isotropic viscoplastic behaviour with several kinematic variables following the Amstrong-Frederic evolution law is described here

The behaviour is described by a standard split of the strain \(\underline{\varepsilon}^{\mathrm{to}}\) in an elastic and a plastic parts, respectively denoted \(\underline{\varepsilon}^{\mathrm{el}}\) and \(\underline{\varepsilon}^{\mathrm{vis}}\):

\[ \underline{\varepsilon}^{\mathrm{to}}=\underline{\varepsilon}^{\mathrm{el}}+\underline{\varepsilon}^{\mathrm{vis}} \]

Elastic behaviour

The stress \(\underline{\sigma}\) is related to the the elastic strain \(\underline{\varepsilon}^{\mathrm{el}}\) by a the standard Hooke behaviour:

\[ \underline{\sigma}= \lambda\,{\mathrm{tr}{\left(\underline{\varepsilon}^{\mathrm{el}}\right)}}\,\underline{I}+2\,\mu\,\underline{\varepsilon}^{\mathrm{el}} \]

Viscoplastic behaviour

The viscoplastic behaviour follows a standard viscoplastic behaviour: \[ \underline{\dot{\varepsilon}}^{\mathrm{vis}}=\left\langle{{\displaystyle \frac{\displaystyle F}{\displaystyle K}}}\right\rangle^{m}\,\underline{n}=\dot{p}\,\underline{n} \]

where \(F\) is the yield surface defined below, \(<.>\) is Macaulay brackets, \(\underline{n}\) is the normal to \(F\) with respect to the stress and \(p\) is the equivalent plastic strain.

The yield surface is defined by: \[ F{\left(\underline{\sigma},\underline{X}_{i},p\right)}={\left(\underline{\sigma}-\sum_{i=1}^{N}\underline{X}_{i}\right)}_{\mathrm{eq}}-R{\left(p\right)}=s^{e}_{\mathrm{eq}}-R{\left(p\right)} \]

where:

• \(R{\left(p\right)}\) describes the isotropic hardening as a function of the equivalent viscoplastic strain \(p\).
• the \(N\) tensors \(\underline{X}_{i}\) (i) are backstresses describing the kinematic hardening.
• \({\left(.\right)}_{\mathrm{eq}}\) is the Von Mises norm.

We have introduced an effective deviatoric stress \(\underline{s}^{e}\) defined by: \[ \underline{s}^{e}=\underline{s}-\sum_{i=1}^{N}\underline{X}_{i} \] where \(\underline{s}\) is the deviatoric part of the stress.

The normal is then given by: \[ \underline{n}={\displaystyle \frac{\displaystyle \partial F}{\displaystyle \partial \underline{\sigma}}}={{\displaystyle \frac{\displaystyle 3}{\displaystyle 2}}}\,{{\displaystyle \frac{\displaystyle \underline{s}^{e}}{\displaystyle s^{e}_{\mathrm{eq}}}}} \]

Evolution of the isotropic hardening

The isotropic hardening is defined by: \[ R{\left(p\right)}=R_{\infty} + {\left(R_{0}-R_{\infty}\right)}\,\exp{\left(-b\,p\right)} \]

Evolution of the kinematic hardenings

\[ \underline{X}_{i}={{\displaystyle \frac{\displaystyle 2}{\displaystyle 3}}}\,C_{i}\,\underline{a}_{i} \]

The evolution of the kinematic variables \(\underline{a}_{i}\) follows the Armstrong-Frederic rule:

\[ \underline{\dot{a}}_{i}=\underline{\dot{\varepsilon}}^{\mathrm{vis}}-g[i]\,\underline{a}_{i}\,\dot{p}=\dot{p}\,{\left(\underline{n}-g[i]\,\underline{a}_{i}\right)} \]

Third MFront Users Day

CEA and EDF are pleased to announce that the third MFront users meeting will take place on May 30th 2017 and will be organized by CEA DEC/SESC at CEA Saclay in the DIGITEO building (building 565, room 34).

Researchers and engineers willing to present their works are welcome.

They may contact the organizers for information at: .

Registration by sending an email at the previous address before May 12th is required to ensure proper organization.

Announcing the tfel-plot project

The tfel-plot project is meant to create:

• a C++11 library for generating 2D plots based on the Qt library (version 4 or version 5).
• a drop-in replacement of gnuplot called tplot.

This project is based on:

• The TFEL libraries.
• The Qt framework .

Compared to gnuplot, we wanted to introduced the following new features:

• The ability to select a curve and modify its properties (color, line width, line style, etc..) interactively.
• The ability to use tplot from the command line.
• A widget that can be used in every Qt code.
• The ability to load C functions in shared libraries, such a the ones generated by the MFront code generator.
• Usage of some features introduced by the TFEL project such as:
  • kriging interpolation.
  • the ability to differentiate functions using the diff operator.
• Support for themes.

More details can be found on the dedicated github page:

https://github.com/thelfer/tfel-plot

[MFront Gallery] Description of the implementation of a simple orthotropic behaviour (27/01/2017)

A new example has been added in the gallery here.

This example describes a simple orthotropic behaviour.

The behaviour is described by a standard split of the strain \(\underline{\varepsilon}^{\mathrm{to}}\) in an elastic and a plastic parts, respectively denoted \(\underline{\varepsilon}^{\mathrm{el}}\) and \(\underline{\varepsilon}^{\mathrm{p}}\):

\[ \underline{\varepsilon}^{\mathrm{to}}=\underline{\varepsilon}^{\mathrm{el}}+\underline{\varepsilon}^{\mathrm{p}} \]

Elastic behaviour

The stress \(\underline{\sigma}\) is related to the the elastic strain \(\underline{\varepsilon}^{\mathrm{el}}\) by a the orthotropic elastic stiffness \(\underline{\underline{\mathbf{D}}}\):

\[ \underline{\sigma}= \underline{\underline{\mathbf{D}}}\,\colon\,\underline{\varepsilon}^{\mathrm{el}} \]

The plastic part of the behaviour is described by the following yield surface: \[ f{\left(\sigma_{H},p\right)} = \sigma_{H}-\sigma_{0}-R\,p \]

where \(\sigma_{H}\) is the Hill stress defined below, \(p\) is the equivalent plastic strain. \(\sigma_{0}\) is the yield stress and \(R\) is the hardening slope.

The Hill stress \(\sigma_{H}\) is defined using the fourth order Hill tensor \(H\): \[ \sigma_{H}=\sqrt{\underline{\sigma}\,\colon\,\underline{\underline{\mathbf{H}}}\colon\,\underline{\sigma}} \]

The plastic flow is assumed to be associated, so the flow direction \(\underline{n}\) is given by \({\displaystyle \frac{\displaystyle \partial f}{\displaystyle \partial \underline{\sigma}}}\):

\[ \underline{n} = {\displaystyle \frac{\displaystyle \partial f}{\displaystyle \partial \underline{\sigma}}} = {{\displaystyle \frac{\displaystyle 1}{\displaystyle \sigma_{H}}}}\,\underline{\underline{\mathbf{H}}}\,\colon\,\underline{\sigma} \]

New eigensolvers (23/01/2017)

The default eigen solver for symmetric tensors used in TFEL is based on analitical computations of the eigen values and eigen vectors. Such computations are more efficient but less accurate than the iterative Jacobi algorithm (see [8, 9]).

With the courtesy of Joachim Kopp, we have introduced the following algorithms:

• Jacobi
• QL with implicit shifts
• Cuppen
• Analytical
• Hybrid
• Householder reduction

The implementation of Joachim Kopp have been updated for C++-11 and make more generic (support of all the floatting point numbers, different types of matrix/vector objects). The algorithms have been put in a separate namespace called fses (Fast Symmetric Eigen Solver) and is independant of the rest of TFEL.

We have also introduced the Jacobi implementation of the Geometric Tools library (see [10, 11]).

Those algorithms are available in 3D. For 2D symmetric tensors, we fall back to some default algorithm as described below.

The various eigen solvers available are enumerated in Table 1.

The eigen solver is passed as a template argument of the computeEigenValues or the computeEigenVectors methods as illustrated in the code below:

tmatrix<3u,3u,real> m2;
tvector<3u,real>    vp2;
std::tie(vp,m)=s.computeEigenVectors<Stensor::GTESYMMETRICQREIGENSOLVER>();

Some benchmarks

We have compared the available algorithm on \(10^{6}\) random symmetric tensors whose components are in \([-1:1]\).

For a given symmetric tensor, we consider that the computation of the eigenvalues and eigenvectors failed if: \[ \Delta_{\infty}=\max_{i\in[1,2,3]}\left\|\underline{s}\,\cdot\,\vec{v}_{i}-\lambda_{i}\,\vec{v}_{i}\right\|>10\,\varepsilon \] where \(\varepsilon\) is the accuracy of the floatting point considered.

The results of those tests are reported on Table 2:

• The standard eigen solver available in previous versions of TFEL offers a very interesting compromise between accuracy and numerical efficiency.
• If very accurate results are required, the FSESJACOBIEIGENSOLVER eigen solver is a good choice.

Official port of TFEL for FreeBSD (20/01/2017)

Thanks to the work of Pedro F. Giffuni , an official port of TFEL/MFront is available for FreeBSD:

http://www.freshports.org/science/tfel/

To install an executable package, you can now simply do:

pkg install tfel-mfront

Alternativel, to build and install TFEL from the ports tree, one can do:

cd /usr/ports/science/tfel/
make
make install

New hyper(visco)elastic behaviours in the MFront model repository (13/01/2017)

The implementation of the Ogden behaviour is now described in depth in the following page:

http://tfel.sourceforge.net/ogden.html

This behaviour is interesting as it highlights the features introduced in TFEL-3.0 for computing isotropic functions of symmetric tensors.

This page uses the formal developments detailled in:

http://tfel.sourceforge.net/hyperelasticity.html

Concerning hyperviscoelasticity, a page describing a generic implementation is available here:

http://tfel.sourceforge.net/hyperviscoelasticity.html

If you have particular wishes on behaviours implementation that you would like to see treated, do not hesitate to send a message at .

MFront model repository (7/01/2017)

A page referencing examples of well written mechanical behaviours has been created here:

http://tfel.sourceforge.net/gallery.html

For each behaviours, we will try to provide tutorial-like pages explaining the implementations details (usage of tensorial objects, special functions of the TFEL library, choice of the algorithms, and so on…)

The first attempt is an hyperelastic behaviour already available in Code_Aster: the Signorini behaviour. You can find the page here:

http://tfel.sourceforge.net/signorini.html

This is still under review, so corrections and feed-backs would be greatly appreciated. The following behaviours are planned to be addressed:

• the Ogden hyperelastic behaviour which will show how we can compute eigenvalues, eigenvectors and isotropic functions of symmetric tensors.
• hyperviscoelasticity (a very small extension of hyperelasticity, indeed)
• simple plastic behaviours

If you have particular wishes on behaviours implementation that you would like to see treated, do not hesitate to send a message at .

TFEL version 3.0 has been released the 16/12/2016.

From a user point of view, TFEL 3.0 brings many game-changing features:

• New mechanical behaviour interfaces to several finite element solvers (Europlexus, Abaqus/Standard, Abaqus/Explicit, CalculiX)
• The support of behaviours bricks.
• The ability to simulate pipes using a rigourous finite strain framework in MTest.
• The introduction of various accelerations algorithms used for solving the mechanical equilibrium when the consistent tangent operator is not available.
• The development of a stable API (application programming interface) in C++ and python which allow building external tools upon MFront and MTest. This point is illustrated by the development by EDF MMC in the Material Ageing Plateform of a new identification tool which is particularly interesting.

Many improvements for mechanical behaviours have also been made:

• Definition and automatic computation of elastic material properties from external MFront files.
• Support for the automatic computation of the thermal expansion and swelling in the mechanical behaviour.
• Better support for orthotropic behaviours with the notion of orthotropic convention which affects various keywords (@ComputeStiffnessTensor, @ComputeThermalExpansion, @Swelling, @AxialGrowth, @HillTensor etc..).
• An initial support of non local mechanical behaviours.
• Time steps management from the mechanical behaviour.
• Consistent tangent operator support in the Cast3M interface.
• Easier computations of isotropic functions of symmetric tensors and their derivatives.
• New material properties interfaces for various programming languages (fortran03, java, GNU/Octave).

A detailed version of the release notes is available here.

A new behaviour implementation, called UnilateralMazars (1 June 2016)

A new behaviour implementation has been submitted by F. Hamon (EDF R&D AMA). This behaviour describes the damaging behaviour of concrete with unilateral effects as described in a dedicated paper:

A new 3D damage model for concrete under monotonic, cyclic and dynamic loadings. Jacky Mazars, François Hamon and Stéphane Grange. Materials and Structures ISSN 1359-5997 DOI 10.1617/s11527-014-0439-8

This implementation can be found in the current development sources of MFront.

Progress in the Abaqus Explicit interface (VUMAT) (28 May 2016)

The Abaqus Explicit interface is becoming quite usable du to the extensive testing efforts of D. Deloison (Airbus). Here is an example a punching test (This test was also modelled using Abaqus Standard).

Documentation of behaviour bricks (27 May 2016)

@Brick "StandardElasticity";

Behaviour bricks will be one of the most important new feature of TFEL 3.0.

A dedicated page has been created here

The EUROPLEXUS interface (27 May 2016)

An interface for the EUROPLEXUS explicit finite element solver has been developed.

EUROPLEXUS (EPX) is a simulation software dedicated to the analysis of fast transient phenomena involving structures and fluids in interaction.

See the dedicated page for more information.

tfel-doc github repository. Talks of the Second MFront Users Day (27 May 2016)

A github repository has been set up to store various documents describing TFEL and MFront usage. The talks of the first and second MFront Users Days are available there:

https://github.com/thelfer/tfel-doc

TFEL github repository (27 May 2016)

The subversion repository used by CEA and EDF are now synchronized with a public githbub repository:

https://github.com/thelfer/tfel

All the branches, commit description and history of TFEL are available. This repository is read-only. Its purpose is to integrate TFEL in continous-integration projects which depends on TFEL.

Announcing the mfront module (May 2016)

A new python module has been introduced to analyse MFront files.

An overview of the module is available here.

Here is a typical usage example:

import mfront

dsl = mfront.getDSL("Chaboche.mfront")
dsl.setInterfaces(["aster"])
dsl.analyseFile("Chaboche.mfront",[])

# file description
fd = dsl.getFileDescription()
print("file author:      ", fd.authorName)
print("file date:        ", fd.date)
print("file descrption:\n", fd.description)

# targets information
tgt = dsl.getTargetsDescription()

# loop over (to be) generated libraries
for l in tgt:
    print(l)

Cast3m 2016 is out (28 April 2016)

Cast3M 2016 has been released.

This version allow even better integration with MFront and can now directly be used to make direct calls to MFront libraries for material properties (mechanical behaviours can be used since Cast3M 2015).

This syntax is now officially supported:

Ty = 'TABLE' ;
Ty.'LIB_LOI'   = 'libCastemM5.so' ;
Ty.'FCT_LOI'   = 'M5_YoungModulus' ;
Ty.'VARIABLES' = 'MOTS' 'T';

mo = 'MODELISER' m 'MECANIQUE' 'ELASTIQUE';
ma = 'MATERIAU' mo 'YOUN' Ty 'NU' 0.3;

A binary version of TFEL compiled for Cast3M 2016 is now available for download on sourceforge:

https://sourceforge.net/projects/tfel/files/

Second MFront Users Day

CEA and EDF are pleased to announce that the second MFront users meeting will take place on May 20th 2016 and will be organized by EDF R&D at the EDF Lab Paris Saclay location.

Researchers and engineers willing to present their works are welcome. They may contact the organizers for information at: .

This users day will take place on Friday, May 20th, 2016 at EDF Lab Paris-Saclay (access map).

Registration is required to ensure proper organization. See the dedicated form on the Code_Aster website: http://www.code-aster.org/spip.php?article906

Abaqus interface

The current development version now includes an experimental interface to the Abaqus solver through the umat subroutine.

The following results shows the results obtained on notched beam under a cyclic loading with an isotropic hardening plastic beahviour implemented with mfront:

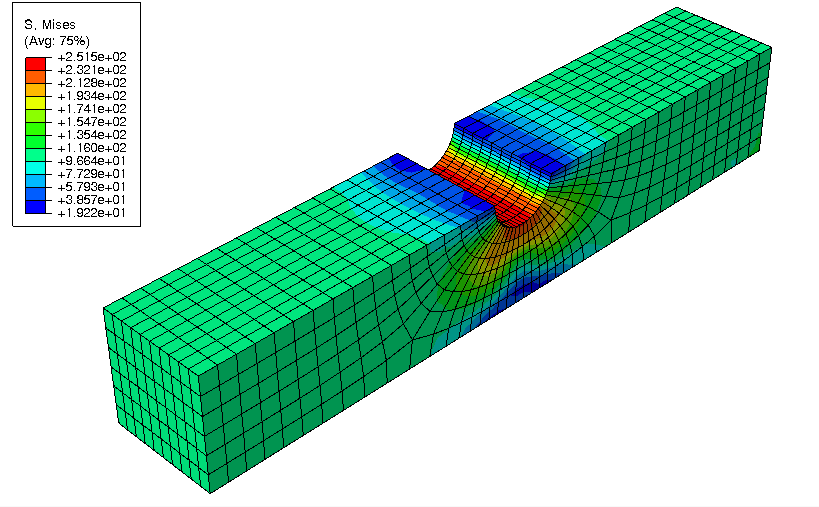
The mfront results can be compared to the results obtained using Abaqus in-built model on the following figure:

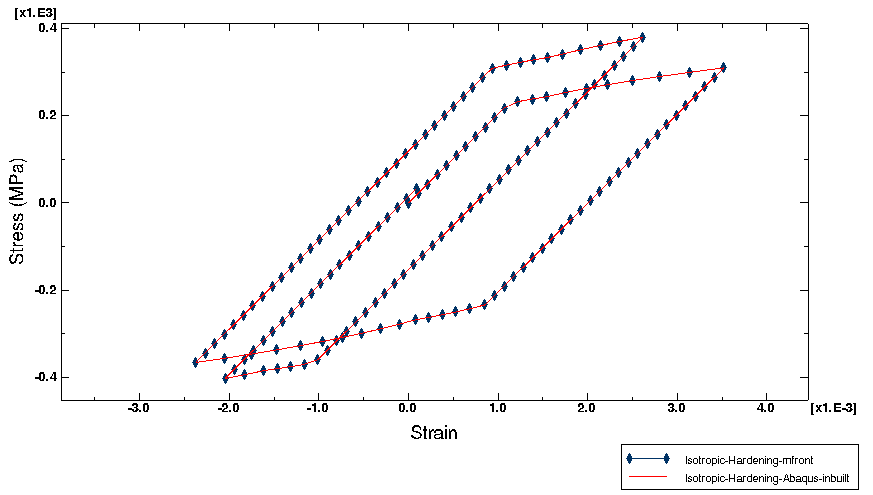
The Abaqus interface is still in its early stage of developments. A full description of its usage and current abilities can be found in the associated documentation.

Feed-back from users would be greatly welcomed.

IMSIA Seminar about MFront on Januar, 27 2016

An IMSIA seminar about MFront will be held on Januar, 27 2016. Here is the official announcement (in french):

Séminaire IMSIA : Implémentation de lois de comportement mécanique à l’aide du générateur de code MFront

Créé dans le cadre de la simulation des éléments combustibles nucléaire au sein d’une plate-forme logicielle nommée PLEIADES, MFront est un générateur de code, distribué en open-source [1], qui vise à permettre aux ingénieurs/chercheurs d’implémenter de manière simple et rapide des lois de comportements mécaniques de manière indépendante du code cible (EF ou FTT) [2,3].

Ce dernier point permet d’échanger les lois MFront entre différents partenaires, universitaires ou industriels. Le lien vers les codes cible se fait via la notion d’interface. A l’heure actuelle, des interfaces existent pour les codes Cast3M, Code-Aster, Abaqus, ZeBuLoN, AMITEX_FFT et d’autres codes métiers, et sont en cours de développement pour d’autres codes tels Europlexus, …

Ce séminaire proposera une description des fonctionnalités de MFront (lois en transformations infinitésimales et en grandes transformations, modèles de zones cohésives) et commentera plusieurs exemples d’applications, discutera des performances numériques obtenues et soulèvera la question de la portabilité des connaissances matériau. Nous montrerons qu’une démarche cohérente allant des expérimentations aux codes de calcul est nécessaire.

[1] http://tfel.sourceforge.net

[2] Introducing the open-source mfront code generator: Application to mechanical behaviours and material knowledge management within the PLEIADES fuel element modelling platform. Thomas Helfer, Bruno Michel, Jean-Michel Proix, Maxime Salvo, Jérôme Sercombe, Michel Casella, Computers & Mathematics with Applications, Volume 70, Issue 5, September 2015, Pages 994-1023, ISSN 0898-1221, http://dx.doi.org/10.1016/j.camwa.2015.06.027.

[3] Implantation de lois de comportement mécanique à l’aide de MFront : simplicité, efficacité, robustesse et portabilité. T. Helfer, J.M. Proix, O. Fandeur. 12ème Colloque National en Calcul des Structures 18-22 Mai 2015, Giens (Var)

MFront and Cyrano3 at the LWR Fuel Performance Meeting 2015 (13 - 17 September 2015, Zurich, Switzerland)

A poster describing the use of MFront in EDF Cyrano3 fuel performance code has been presented at the LWR Fuel Performance Meeting 2015 (13 - 17 September 2015, Zurich, Switzerland):

• abstract
• poster

Release of version 2.0.3 (9 September 2015)

Version 2.0.3 is mostly a bug-fix release:

• Fix of a minor bug in the CxxTokenizer class which was appears when using the clang libc++ standard library. This prevented many MTest tests to work on Mac OS X.
• Fix of Ticket #9
• Fix of Ticket #10
• Fix of Ticket #11
• The class ExternalBehaviourDescription was introduced
• The AxialGrowth entry was added to the glossary

A full description of the 2.0.3 release can be found here (in french).

Introducting mfront-doc (19 August 2015)

mfront-doc allows the user to extract the documentation out of MFront file. mfront-doc generates files in pandoc markdown format. Those files can be processed using pandoc and be converted to one of the many file format supported by pandoc, including LaTeX, html or various Word processor formats: Microsoft Word docx, OpenOffice/LibreOffice ODT.

mfront-doc is developped in the 3.0.x branche of TFEL. A overview of the mfront-doc functionalities can be found here.

New documentations pages (18 August 2015)

New documentation pages were added to describe the MTest and MFront keywords:

• MFront keywords, sorted by domain specific languages:
  • DefaultDSL
  • DefaultCZMDSL
  • DefaultFiniteStrainDSL
  • Implicit
  • ImplicitFiniteStrain
  • ImplicitII
  • IsotropicMisesCreep
  • IsotropicPlasticMisesFlow
  • IsotropicStrainHardeningMisesCreep
  • MaterialLaw
  • Model
  • MultipleIsotropicMisesFlows
  • RungeKutta
• MTest keywords

New interfaces for material properties (July 2015)

The current development version of MFront includes two new interfaces for material properties:

• java designed for the java language.
• octave designed for GNU Octave which is a high-level interpreted language, primarily intended for numerical computations.

Here is an example of a GNU Octave session used to compute the Young Modulus of uranium-plutonium carbide \(UPuC\) for various porosities over a range of temperatures:

octave:1> T=[300:100:1500]
T =
    300    400    500    600    700    800    900   1000   1100   1200   1300   1400   1500
octave:2> y01=UPuC_YoungModulus(T,0.1)
y01 =
   1.7025e+11   1.6888e+11   1.6752e+11   1.6616e+11   1.6480e+11   1.6344e+11   1.6207e+11   1.6071e+11   1.5935e+11   1.5799e+11   1.5662e+11   1.5526e+11   1.5390e+11
octave:3> y02=UPuC_YoungModulus(T,0.2)
y02 =
   1.1853e+11   1.1758e+11   1.1663e+11   1.1568e+11   1.1474e+11   1.1379e+11   1.1284e+11   1.1189e+11   1.1094e+11   1.0999e+11   1.0905e+11   1.0810e+11   1.0715e+11

A “publications” page has been added to the website (July 2015)

The number of papers in which MFront is used is increasing. A dedicated page has been added here.

If you publish papers which refers to MFront, please consider contributing to this page.

The paper entitled “Introducing the open-source MFront code generator …” has been accepted for publication in Computers and Mathematics with Applications (24 june 2015)

The first paper dedicated to MFront, written by Thomas Helfer, Bruno Michel, Jean-Michel Proix, Maxime Salvo, Jérôme Sercombe, and Michel Casella, has been accepted Computers and Mathematics with Applications. The paper is available online on the sciencedirect website:

http://www.sciencedirect.com/science/article/pii/S0898122115003132

The PLEIADES software environment is devoted to the thermomechanical simulation of nuclear fuel elements behaviour under irradiation. This platform is co-developed in the framework of a research cooperative program between Électricité de France (EDF), AREVA and the French Atomic Energy Commission (CEA). As many thermomechanical solvers are used within the platform, one of the PLEAIADES’s main challenge is to propose a unified software environment for capitalisation of material knowledge coming from research and development programs on various nuclear systems.

This paper introduces a tool called mfront which is basically a code generator based on C++ (Stroustrup and Eberhardt, 2004). Domain specific languages are provided which were designed to simplify the implementations of new material properties, mechanical behaviours and simple material models. mfront was recently released under the GPL open-source licence and is available on its web site: http://tfel.sourceforge.net/.

The authors hope that it will prove useful for researchers and engineers, in particular in the field of solid mechanics. mfront interfaces generate code specific to each solver and language considered.

In this paper, after a general overview of mfront functionalities, a particular focus is made on mechanical behaviours which are by essence more complex and may have significant impact on the numerical performances of mechanical simulations. mfront users can describe all kinds of mechanical phenomena, such as viscoplasticity, plasticity and damage, for various types of mechanical behaviour (small strain or finite strain behaviour, cohesive zone models). Performance benchmarks, performed using the Code-Aster finite element solver, show that the code generated using mfront is in most cases on par or better than the behaviour implementations written in fortran natively available in this solver. The material knowledge management strategy that was set up within the PLEIADES platform is briefly discussed. A material database named sirius proposes a rigorous material verification workflow.

We illustrate the use of mfront through two case of studies: a simple FFC single crystal viscoplastic behaviour and the implementation of a recent behaviour for the fuel material which describes various phenomena: fuel cracking, plasticity and viscoplasticity.

Castem 2015 is out (12 April 2015)

Cast3M 2015 has been released.

This release allow direct call to MFront libraries for mechanical behaviours. The following syntax of the MODELISER operator is now officially supported:

mod1 = 'MODELISER' s1 'MECANIQUE' 'ELASTIQUE' 'ISOTROPE'
   'NON_LINEAIRE' 'UTILISATEUR'
   'LIB_LOI' 'src/libUmatBehaviour.so'
   'FCT_LOI' 'umatnorton'
   'C_MATERIAU' coel2D
   'C_VARINTER' stav2D
   'PARA_LOI'   para2D
   'CONS' M;

See the dedicated page for more information.

Salome-Meca 2015.1 is out (1O April 2015)

Salome-Meca 2015.1, which combines the Salome platform and Code-Aster, has been released on 1O April 2015. This version is the first to include a pre-packaged version of TFEL (version 2.0.1).

Salome-Meca and Code_Aster Users Day (26 March 2015)

A presentation of MFront was done during the Salome-Meca and Code_Aster Users Day 2015 user meeting at EDF Lab Clamart.

Slides can be found here.

MFront user meeting (6 Februar 2015)

The first MFront user meeting was held in Cadarache on Februar,6 2015. 27 participants from CEA, EDF, Areva and CNRS could discuss and comment about their use of MFront.

Various subjects were discussed:

• Introduction to the user meeting
• New functionalities introduced in TFEL/MFront 2.0
• Feed-back from users:
  • Feed-back from the Code-Aster development team
  • Feed-back from the Cyrano3 development team
• Modèle de couplage Fluage/Endommagement/Réaction Alcali Granulat (RAG) du béton
• Modélisation à différentes échelles du comportement mécanique du dioxyde d’uranium
• Writing portable behaviour with MFront
• On the road to TFEL 3.x

Those talks are available here

First MFront user meeting (12 December 2014)

We are glad to announce that the first MFront user meeting will be held in Cadarache on Februar,6 2015. Everyone is invited but a registration must be performed before Januar, 16 2015 ().

Various subjects are already planned:

• New functionalities introduced in TFEL/MFront 2.0
• Feed-back from users:
  • Feed-back from the Code-Aster development team
  • Feed-back from the Cyrano3 development team
• MFront usage for concrete modelling
• Examples of MFront usage in finite strain analyses
• Application of MFront to nuclear fuel modelling
• How to write portable behaviour implementations ?
• Conclusions

Other talks are welcomed.

Some applications of MFront at the Cast3M user meeting (4 December 2014)

The Cast3M user meeting was held in Paris on November 28, 2014. Jérémy Hure had a talk about the application of MFront in finite strain elasto-plasticity. This talk is available here.

AMITEX_FFTP has its own website (4 December 2014)

AMITEX_FFTP has now its own dedicated webiste.

The main purpose of AMITEX_FFTP is to implement an efficient distributed mechanical solver based on Fast Fourier Transform. AMITEX_FFTP is developped by CEA in the Departement of Nuclear Material.

AMITEX_FFTP is distributed under a free license for research and education purpose.

Release of TFEL version 2.0.1 (2 December 2014)

TFEL version 2.0.1 is now available. This is mainly a bug-fix release after version 2.0.0.

This version is meant to be used in Code-Aster version 12.3 that will be released in January 2015.

Creation of the address (1 December 2014)

A new contact address has been created: .

This address can be used to contact directly the developers of TFEL and MFront for specific issues. However, if your issue may interest a broader audience, you may want to send a post to the TFEL users mailing lists: .

MFront talk at Materiaux 2014 Montpellier (24 November 2014)

An MFront talk was given at Materiaux 2014. Slides (in french) are available here.

Beta release of tfel-2.0.1 for Windows 64bits and Cast3M 2014 (18 November 2014)

A beta version of tfel-2.0.1 for Windows 64bits and Cast3M 2014 has been released. A binary installer is provided here.

Installing this version requires a functional installation of Cast3M \(2014\) (which shall be patched to call external libraries) and the MSYS shell (It is recommended not to install mingw compilers along with the MSYS shell as Cast3M provides its own version of those compilers).

Installation instructions of those requirements are available here.

Any feedback would be gratefully acknowledge.

Note: The binary provided requires the mingw libraries delivered with Cast3M 2014.

Note: A standalone version of tfel-2.0.1 will be provided shortly.

MFront behaviours can now be used in AMITEX_FFTP (24 October 2014)

AMITEX_FFTP is a massively parallel mechanical solver based on FFT developed at CEA. MFront behaviours can be used in AMITEX_FFTP through the UMAT interface introduced by the Cast3M finite element solver.

TFEL/MFront on Cast3M web site (15 October 2014)

A page dedicated to MFront is now available on the Cast3M web site.

Release of TFEL 2.0 (1 October 2014)

Here is the official announcement by Jean-Paul DEFFAIN (in French):

Bonjour,

Une version libre de MFront est désormais officiellement disponible sous licence GPL et CECILL-A.

Cette version 2.0 permet entre autres de générer des lois de comportements en transformations infinitésimales et en grandes transformations ainsi que des modèles de zones cohésives. Les lois générées sont utilisables dans les codes aux éléments finis Cast3M, Code-Aster, ZeBuLoN, l’ensemble des applications développées dans la plateforme PLEIADES, notamment Cyrano3, et le solveur FFT de la plate-forme. Des interfaces vers d’autres codes peuvent être rajoutées.

Un projet dédié a été crée sur sourceforge (http://sourceforge.net/projects/tfel) et fournit :

• un site dédié (http://tfel.sourceforge.net)
• un espace de téléchargement (http://sourceforge.net/projects/tfel/files) qui permet d’accéder à la version 2.0
• les listes de diffusion tfel-announce et tfel-discuss (http://sourceforge.net/p/tfel/tfel)
• un forum (http://sourceforge.net/p/tfel/discussion)
• un outil de demande d’évolution et de déclaration de bugs par tickets (http://sourceforge.net/p/tfel/tickets)

Pour les personnes souhaitant contribuer au développement, le dépôt subversion est accessible sur le serveur:

https://svn-pleiades.cea.fr/SVN/TFEL

L’accès à ce dépôt est restreint mais nécessite l’ouverture d’un compte spécifique sur demande au .

Nous remercions chaleureusement tous ceux qui ont contribué à cette version et invitons toutes les personnes intéressées à se joindre au développement de MFront.

Jean-Paul DEFFAIN

Chef du programme SIMU

Commissariat à l’Énergie Atomique

References