The page describes the new functionalities of Version 3.4 of the TFEL project.

1 Overview

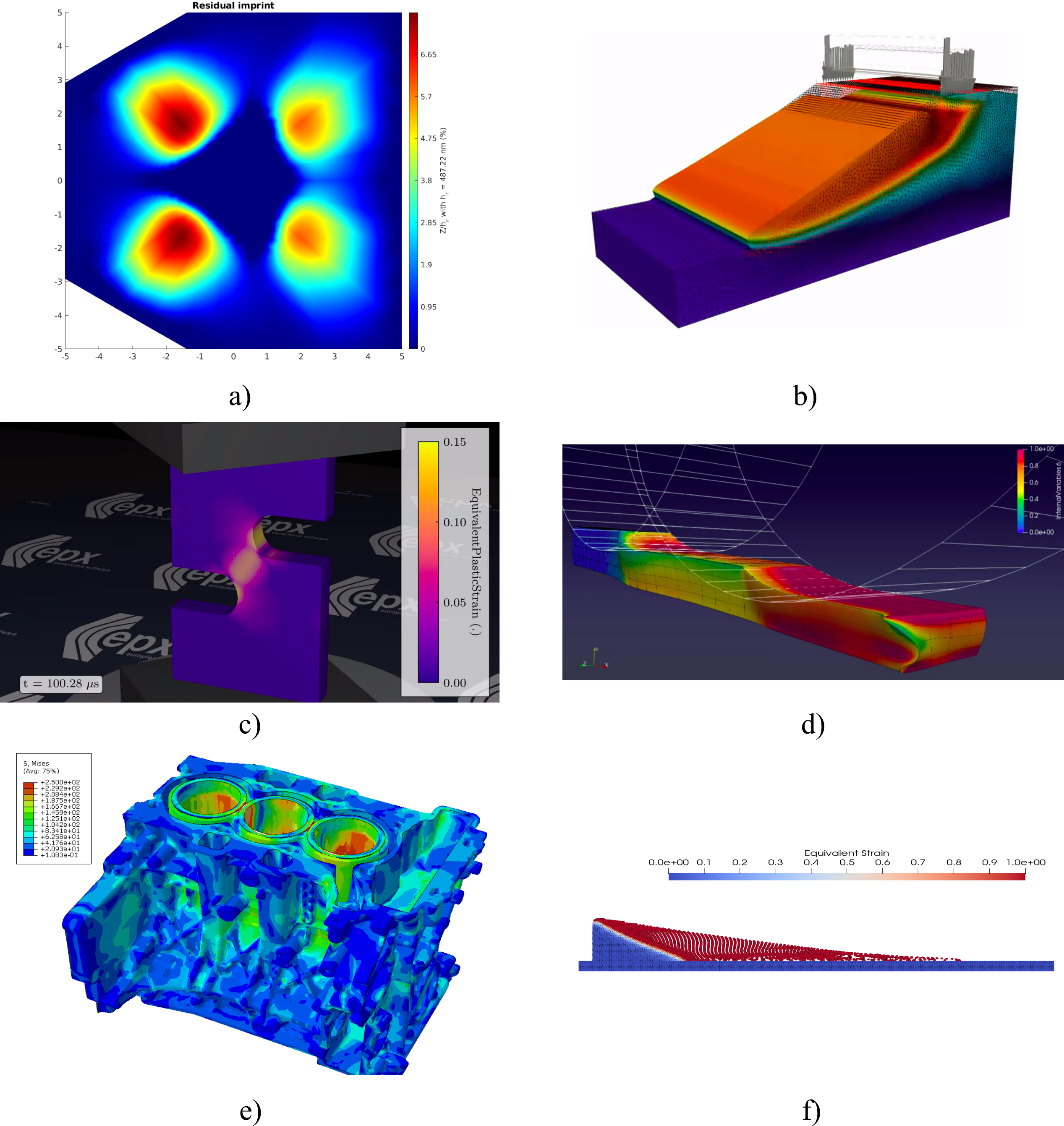
1.1 Some noticeable applications of MFront and MGIS in 2020

Figure 1 presents some noticeable applications of MFront:

1. Normalised residual topography after an indentation test on a single crsytal of copper with Méric-Cailletaud’ finite stain behaviour [1] using Ansys. Contribution of A. Bourceret and A. Lejeune, (FEMTO).
2. Slope failure analysis with strength reduction in OpenGeoSys [2]. Contribution of T. Deng and T. Nagel (Geotechnical Institute, Technische Universität Bergakademie Freiberg).
3. Integration of the MGIS integration in Europlexus. Contribution of P. Bouda, (CEA DM2S).
4. Simulation of rolling using the innovative CEA’ proto-application MEFISTO. Contribution of O. Jamond, (CEA DM2S).
5. Industrial thermomechanical design of a cylinder block with an with MFront and Abaqus at Groupe PSA. This study is one result of the PhD thesis of L. Jacquinot which provides a continuous modelling of the AlSi9Cu3Mg aluminium alloy behaviour from manufacturing to final usage Contribution of A. Forré (Groupe PSA).
6. Column collapse using the Material Point Method. Contribution of Ning Guo, Wenlong Li (Zhejiang University)

1.2 Highlights

The major features of Version 3.4 are:

• A better support generalised behaviours, in particular regarding the computation of the consistent tangent operator in the implicit schemes [3]. Examples of this features are presented in references [4–7].
• An extension of the StandardElastoViscoPlasticity brick to porous materials See Figure 2 for some examples of ductile failure simulations with Cast3M.
• The ability to store MFront behaviours in a madnex file. madnex is a data model based on HDF5 file format that was originally designed by EDF as part of their in-house projects for capitalising their experimental data and which is now being shared among the main actors of the french nuclear industry with the aim of becoming the de facto standard to exchange experimental data, MFront implementations and unit tests of those implementations. Documentation is available here: http://tfel.sourceforge.net/madnex.html.
• The MFront’ generic interface now exports functions to rotate gradients in the material frame before the behaviour integration and rotate the thermodynamics forces and the tangent operator blocks in the global frame after the behaviour integration. Such functions are particularly useful for generalised behaviours.

A special effort has been set on the documentation with many new tutorials [[3];[4];[5];[8];[6];[9];[10];[11];@;[7]].

In order to increase the community of developers, a first tutorial showing how a new stress criteria can be added to the StandardElastoViscoPlasticity brick has been published [12]. Other similar tutorials are being considered.

1.3 Simultaneous releases This version has been released along with:

• Version 3.0.6
• Version 3.1.6
• Version 3.2.3
• Version 3.3.1

Those releases are mainly related to bug-fixes. Version 3.4 inherits from all the fixes detailed in the associated release notes.

1.4 Known incompatibilities

1.4.1 getPartialJacobianInvert

In previous versions, getPartialJacobianInvert was implemented as a method.

This may broke the code, in the extremely unlikely case, that the call to getPartialJacobianInvert was explicitly qualified as a method, i.e. if it was preceded by the this pointer. Hence, the following statement is not more valid:

this->getPartialJacobianInvert(Je);

To the best of our knowledge, no implementation is affected by this incompatibility.

1.4.2 Declaration of the offsets of the integration variables in implicit schemes

The offsets of the integration variables in implicit schemes are now automatically declared in the @Integrator code block. The names of the variables associated with those offsets may conflict with user defined variables. See Section 4.4.1 for a description of this new feature.

To the best of our knowledge, no implementation is affected by this incompatibility.

1.5 Noticeable fixed issues that may affect the results obtained with previous versions

Ticket #256 reported that the scalar product of two unsymmetric tensors was not properly computed.

This may affect single crystal finite strain computations to a limited extent, as the Mandel stress tensor is almost symmetric.

2 Documentation

This page describes how to extend the TFEL/Material library and the StandardElastoViscoPlasticity brick with a new stress criterion.

3 New features of the TFEL libraries

3.1 New features of the TFEL/Math library

3.1.1 Solving multiple linear systems with TinyMatrixSolve

  tfel::math::tmatrix<4, 4, T> m = {0, 2,  0,  1,  //
                                    2, 2,  3,  2,  //
                                    4, -3, 0,  1,  //
                                    6, 1,  -6, -5};
  tfel::math::tmatrix<4, 2, T> b = {0,  0,    //
                                    -2, -12,  //
                                    -7, -42,  //
                                    6,  36};
  tfel::math::TinyMatrixSolve<4u, T>::exe(m, b);

3.1.2 The DerivativeType metafunction and the derivative_type alias

The DerivativeType metafunction allows requiring the type of the derivative of a mathematical object with respect to another object. This metafunction handles units.

For example:

DerivativeType<StrainStensor, time>::type de_dt;

declares the variable de_dt as the derivative of the a strain tensor with respect to scalare which has the unit of at time.

The derivative_type alias allows a more concise declaration:

derivative_type<StrainStensor, time> de_dt;

In MFront code blocks, the StrainRateStensor typedef is automatically defined, so the previous declaration is equivalent to:

StrainRateStensor de_dt;

The derivative_type is much more general and can be always be used.

3.1.3 Scalar Newton-Raphson algorithm

The function scalarNewtonRaphson, declared in the TFEL/Math/ScalarNewtonRaphson.hxx is a generic implementation of the Newton-Raphson algorithm for scalar non linear equations. The Newton algorithm is coupled with bisection whenever root-bracketing is possible, which considerably increase its robustness.

This implementation handles properly IEEE754 exceptional cases (infinite numbers, NaN values), even if advanced compilers options are used (such as -ffast-math under gcc).

3.1.3.1 Usage

// this lambda takes the current estimate of the root and returns
// a tuple containing the value of the function whose root is searched
// and its derivative.
auto fdf = [](const double x) {
  return std::make_tuple(x * x - 13, 2 * x);
};
// this lambda returns a boolean stating if the algorithm has converged
// the first argument is the value of the function whose root is searched
// the second argument is the Newton correction to be applied
// the third argument is the current estimate of the root
// the fourth argument is the current iteration number
auto c = [](const double f, const double, const double, const int) {
  return std::abs(f) < 1.e-14;
};
// The `scalarNewtonRaphson` returns a tuple containing:
// - a boolean stating if the algorithm has converged
// - the last estimate of the function root
// - the number of iterations performed
// The two last arguments are respectively the initial guess and 
// the maximum number of iterations to be performed
const auto r = tfel::math::scalarNewtonRaphson(fdf, c, 0.1, 100);

4 New features of MFront

4.1 Debugging options

A new command line option has been added to MFront. The -g option adds standard debugging flags to the compiler flags when compiling shared libraries.

4.2 Improved robustness of the isotropic DSLs

The @Flow block can now return a boolean value in the IsotropicMisesCreep, IsotropicMisesPlasticFlow, IsotropicStrainHardeningMisesCreep DSLs.

This allows to check to avoid Newton steps leading to too high values of the equivalent stress by returning false. This usually occurs if in elastic prediction is made (the default), i.e. when the plastic strain increment is too low.

If false is returned, the value of the plastic strain increment is increased by doubling the previous Newton correction. If this happens at the first iteration, the value of the plastic strain increment is set to half of its upper bound value (this upper bound value is such that the associated von Mises stress is null).

4.3 Generic behaviours

4.3.1 Add the possibility of defining the tangent operator blocks: the @TangentOperatorBlock and @TangentOperatorBlocks keywords

In version 3.3.x, some tangent operator blocks are automatically declared, namely, the derivatives of all the fluxes with respect to all the gradients. The @AdditionalTangentOperatorBlock and @AdditionalTangentOperatorBlocks keywords allowed to add tangent operator blocks to this default set.

The @TangentOperatorBlock and @TangentOperatorBlocks allow a more fine grained control of the tangent operator blocks available and disable the use of the default tangent operation blocks. Hence, tangent operator blocks that are structurally zero (for example due to symmetry conditions) don’t have to be computed any more.

4.4 Improvements to the implicit domain specific languages

4.4.1 Automatic definition of the offsets associated with integration variables

Let X be the name of an integration variable. The variable X_offset is now automatically defined in the @Integrator code block.

This variable allows a direct modification of the residual associated with this variable (though the variable fzeros) and jacobian matrix (though the variable jacobian).

4.5 Improvement of the StandardElastoViscoPlasticity brick

4.5.1 Porous (visco-)plasticity

The StandardElastoViscoPlasticity brick has been extended to support porous (visco-)plastic flows which are typically used to model ductile failure of metals. This allows building complex porous plastic models in a clear and concise way, as illustrated below:

@Brick StandardElastoViscoPlasticity{
  stress_potential : "Hooke" {young_modulus : 70e3, poisson_ratio : 0.3},  //
  inelastic_flow : "Plastic" {
    criterion : "GursonTvergaardNeedleman1982" {
      f_c : 0.04, f_r : 0.056, q_1 : 2., q_2 : 1., q_3 : 4.},
    isotropic_hardening : "Linear" {R0 : 274},
    isotropic_hardening : "Voce" {R0 : 0, Rinf : 85, b : 17},
    isotropic_hardening : "Voce" {R0 : 0, Rinf : 17, b : 262}
  }
  nucleation_model : "Chu_Needleman" {
    An : 0.01, pn : 0.1, sn : 0.1 },
};

The following stress criteria are available:

• GursonTvergaardNeedleman1982
• RousselierTanguyBesson2002

The following nucleation models are available:

• ChuNeedleman1980 (strain)
• ChuNeedleman1980 (stress)
• PowerLaw (strain)
• PowerLaw (stress)

This extension will be fully described in a dedicated report which is currently under review.

4.5.2 The HarmonicSumOfNortonHoffViscoplasticFlows inelastic flow

An new inelastic flow called HarmonicSumOfNortonHoffViscoplasticFlows has been added. The equivalent viscoplastic strain rate \(\dot{p}\) is defined as:

\[ \dfrac{1}{\dot{p}}=\sum_{i=1}^{N}\dfrac{1}{\dot{p}_{i}} \]

where \(\dot{p}_{i}\) has an expression similar to the the Norton-Hoff viscoplastic flow:

\[ \dot{p}_{i}=A_{i}\,{\left(\dfrac{\sigma_{\mathrm{eq}}}{K_{i}}\right)}^{n_{i}} \]

4.5.2.1 Example

@Brick StandardElastoViscoPlasticity{
  stress_potential : "Hooke" {young_modulus : 150e9, poisson_ratio : 0.3},
  inelastic_flow : "HarmonicSumOfNortonHoffViscoplasticFlows" {
    criterion : "Mises",
    A : {8e-67, 8e-67},
    K : {1,1},
    n : {8.2,8.2}
  }
};

4.5.3 Choice of the eigen solver for some stress criteria in the StandardElastoviscoPlascity brick

The Hosford1972 and Barlat2004 now has an eigen_solver option. This option may take either one of the following values:

• default: The default eigen solver for symmetric tensors used in TFEL/Math. It is based on analytical computations of the eigen values and eigen vectors. Such computations are numerically more efficient but less accurate than the iterative Jacobi algorithm.
• Jacobi: The iterative Jacobi algorithm (see [13, 14] for details).

4.5.3.1 Example

@Brick StandardElastoViscoPlasticity{
  stress_potential : "Hooke" {young_modulus : 150e9, poisson_ratio : 0.3},
  inelastic_flow : "Plastic" {
    criterion : "Hosford1972" {a : 100, eigen_solver : "Jacobi"},
    isotropic_hardening : "Linear" {R0 : 150e6}
  }
};

4.5.4 Built-in convergence helpers

4.5.4.1 Newton steps rejections based on the change of the flow direction between two successive estimates

Some stress criteria (Hosford 1972, Barlat 2004, Mohr-Coulomb) shows sharp edges that may cause the failure of the standard Newton algorithm, due to oscillations in the prediction of the flow direction.

Rejecting Newton steps leading to a too large variation of the flow direction between the new estimate of the flow direction and the previous estimate is a cheap and efficient method to overcome this issue. This method can be viewed as a bisectional linesearch based on the Newton prediction: the Newton steps magnitude is divided by two if its results to a too large change in the flow direction.

More precisely, the change of the flow direction is estimated by the computation of the cosine of the angle between the two previous estimates:

\[ \cos{\left(\alpha_{\underline{n}}\right)}=\dfrac{\underline{n}\,\colon\,\underline{n}_{p}}{\lVert \underline{n}\rVert\,\lVert \underline{n}\rVert} \]

with \(\lVert \underline{n}\rVert=\sqrt{\underline{n}\,\colon\,\underline{n}}\).

The Newton step is rejected if the value of \(\cos{\left(\alpha_{\underline{n}}\right)}\) is lower than a user defined threshold. This threshold must be in the range \(\left[-1:1\right]\), but due to the slow variation of the cosine near \(0\), a typical value of this threshold is \(0.99\) which is equivalent to impose that the angle between two successive estimates is below \(8\mbox{}^{\circ}\).

4.5.4.1.1 Example

Here is an implementation of a perfectly plastic behaviour based on the Hosford criterion with a very high exponent (\(100\)), which closely approximate the Tresca criterion:

@DSL Implicit;
@Behaviour HosfordPerfectPlasticity100;
@Author Thomas Helfer;
@Description{
  A simple implementation of a perfect plasticity
  behaviour using the Hosford stress.
};

@ModellingHypotheses{".+"};
@Epsilon 1.e-16;
@Theta 1;

@Brick StandardElastoViscoPlasticity{
  stress_potential : "Hooke" {young_modulus : 150e9, poisson_ratio : 0.3},
  inelastic_flow : "Plastic" {
    criterion : "Hosford1972" {a : 100},
    isotropic_hardening : "Linear" {R0 : 150e6},
    cosine_threshold : 0.99
  }
};

4.5.4.2 Maximum equivalent stress in the Plastic flow

During the Newton iterations, the current estimate of the equivalent stress \(\sigma_{\mathrm{eq}}\) may be significantly higher than the elastic limit \(R\). This may lead to a divergence of the Newton algorithm.

One may reject the Newton steps leading to such high values of the elastic limit by specifying a relative threshold denoted \(\alpha\), i.e. if \(\sigma_{\mathrm{eq}}\) is greater than \(\alpha\,\cdot\,R\). A typical value for \(\alpha\) is \(1.5\). This relative threshold is specified by the maximum_equivalent_stress_factor option.

In some cases, rejecting steps may also lead to a divergence of the Newton algorithm, so one may specify a relative threshold \(\beta\) on the iteration number which desactivate this check, i.e. the check is performed only if the current iteration number is below \(\beta\,\cdot\,i_{\max{}}\) where \(i_{\max{}}\) is the maximum number of iterations allowed for the Newton algorithm. A typical value for \(\beta\) is \(0.4\). This relative threshold is specified by the equivalent_stress_check_maximum_iteration_factor option.

4.5.4.2.1 Example

@DSL Implicit;
@Behaviour PerfectPlasticity;
@Author Thomas Helfer;
@Date 17 / 08 / 2020;
@Description{};

@Epsilon 1.e-14;
@Theta 1;

@Brick StandardElastoViscoPlasticity{
  stress_potential : "Hooke" {young_modulus : 200e9, poisson_ratio : 0.3},
  inelastic_flow : "Plastic" {
    criterion : "Mises",
    isotropic_hardening : "Linear" {R0 : 150e6},
    maximum_equivalent_stress_factor : 1.5,
    equivalent_stress_check_maximum_iteration_factor: 0.4
  }
};

4.5.5 The StandardStressCriterionBase and StandardPorousStressCriterionBase base class to ease the extension of the StandardElastoViscoPlasticity brick

4.5.6 The Power isotropic hardening rule

The Power isotropic hardening rule is defined by: \[ R{\left(p\right)}=R_{0}\,{\left(p+p_{0}\right)}^{n} \]

4.5.6.1 Options

The Power isotropic hardening rule expects at least the following material properties:

• R0: the coefficient of the power law
• n: the exponent of the power law

The p0 material property is optional and generally is considered a numerical parameter to avoir an initial infinite derivative of the power law when the exponent is lower than \(1\).

4.5.6.2 Example

The following code can be added in a block defining an inelastic flow:

    isotropic_hardening : "Linear" {R0 : 50e6},
    isotropic_hardening : "Power" {R0 : 120e6, p0 : 1e-8, n : 5.e-2}

4.6 Improvement of the generic interface

4.6.1 Support of orthotropic behaviours

Orthotropic behaviours requires to:

• rotate the gradients in the material frame in the global frame before the behaviour integration.
• rotate the thermodynamic forces and the tangent operator blocks from the material frame in the global frame.

By design, the generic behaviour interface does not automatically perform those rotations as part of the behaviour integration but generates additional functions to do it. This choice allows the calling solver to use their own internal routines to handle the rotations between the global and material frames.

However, the generic interface also generates helper functions which can perform those rotations. Those functions are named as follows:

• <behaviour_function_name>_<hypothesis>_rotateGradients
• <behaviour_function_name>_<hypothesis>_rotateThermodynamicForces
• <behaviour_function_name>_<hypothesis>_rotateTangentOperatorBlocks

They all take three arguments:

• a pointer to the location where the rotated variables will be stored.
• a pointer to the location where the original variables are stored.
• a pointer to the rotation matrix from the global frame to the material frame. The rotation matrix has 9 components stored in column-major format. For the function handling the thermodynamic forces and the tangent operators blocks, this rotation matrix is transposed internally to get the rotation matrix from the material frame to the global frame.

In place rotations is explicitly allowed, i.e. the first and second arguments can be a pointer to the same location.

The three previous functions works for an integration point. Three other functions are also generated:

• <behaviour_function_name>_<hypothesis>_rotateArrayOfGradients
• <behaviour_function_name>_<hypothesis>_rotateArrayOfThermodynamicForces
• <behaviour_function_name>_<hypothesis>_rotateArrayOfTangentOperatorBlocks

Those functions takes an additional arguments which is the number of integration points to be treated.

4.6.1.1 Finite strain behaviours

Finite strain behaviours are a special case, because the returned stress measure and the returned tangent operator can be chosen at runtime time. A specific rotation function is generated for each supported stress measure and each supported tangent operator.

Here is the list of the generated functions:

• <behaviour_function_name>_<hypothesis>_rotateThermodynamicForces_CauchyStress. This function assumes that its first argument is the Cauchy stress in the material frame.
• <behaviour_function_name>_<hypothesis>_rotateThermodynamicForces_PK1Stress. This function assumes that its first argument is the first Piola-Kirchhoff stress in the material frame.
• <behaviour_function_name>_<hypothesis>_rotateThermodynamicForces_PK2Stress. This function assumes that its first argument is the second Piola-Kirchhoff stress in the material frame. <behaviour_function_name>_<hypothesis>_rotateTangentOperatorBlocks_dsig_dF. This function assumes that its first argument is the derivative of the Cauchy stress with respect to the deformation gradient in the material frame.
• <behaviour_function_name>_<hypothesis>_rotateTangentOperatorBlocks_dPK1_dF. This function assumes that its first argument is the derivative of the first Piola-Kirchhoff stress with respect to the deformation gradient in the material frame.
• <behaviour_function_name>_<hypothesis>_rotateTangentOperatorBlocks_PK2Stress. This function assumes that its first argument is the derivative of the second Piola-Kirchhoff stress with respect to the Green-Lagrange strain in the material frame.

5 New features in MTest

5.1 Import behaviour parameters

The behaviour parameters are now automatically imported in the behaviour namespace with its default value.

For example, the YoungModulus parameter of the BishopBehaviour will be available in the BishopBehaviour::YoungModulus variable.

This feature is convenient for building unit tests comparing the simulated results with analytical ones.

The list of imported parameters is displayed in debug mode.

5.2 Unicode characters in MTest

Usage of a limited subsets of UTF-8 characters in variable names is now allowed. This subset is described here:

http://tfel.sourceforge.net/unicode.html

6 New features of the python bindings

6.1 Improvements of the tfel.math module

6.1.1 NumPy support

This version is the first to use Boost/NumPy to provide interaction with NumPy array.

Note

The NumPy support is enabled by default if the Python bindings are requested. However, beware that Boost/NumPy is broken for Python3 up to version 1.68. We strongly recommend disabling NumPy support when using previous versions of Boost by passing the flag -Denable-numpy-support=OFF to the cmake invokation.

6.1.2 Exposing acceleration algorithm

The FAnderson and UAnderson acceleration algorithms are now available in the tfel.math module. This requires NumPy support.

6.1.2.1 Example of the usage of the UAnderson acceleration algorithm

The following code computes the solution of the equation \(x=\cos{\left(x\right)}\) using a fixed point algorithm.

from math import cos
import numpy as np
import tfel.math

# The accelerator will be based on
# the 5 last Picard iterations and
# will be performed at every step
a = tfel.math.UAnderson(5,1)

f = lambda x: np.cos(x)
    
x0 = float(10)
x = np.array([x0])    

# This shall be called each time a
# new resolution starts
a.initialize(x)
for i in range(0,100):
    x = f(x)
    print(i, x, f(x[0]))
    if(abs(f(x[0])-x[0])<1.e-14):
        break
    # apply the acceleration
    a.accelerate(x)

Without acceleration, this algorithm takes \(78\) iterations. In comparison, the accelerated algorithm takes \(9\) iterations.

7 tfel-unicode-filt

Version 3.3 introduces unicode support in MFront. This feature significantly improves the readability of MFront files, bringing it even closer to the mathematical expressions.

When generating C++ sources, unicode characters are mangled, i.e. translated into an acceptable form for the C++ compiler. This mangled form may appears in the compiler error message and are difficult to read.

The tfel-unicode-filt tool, which is similar to the famous c++filt tool, can be use to demangle the outputs of the compiler.

For example, the following error message:

$ mfront --obuild  --interface=generic ThermalNorton.mfront
Treating target : all
In file included from ThermalNorton-generic.cxx:33:0:
ThermalNorton.mfront: In member function ‘bool tfel::material::ThermalNorton<hypothesis, Type, false>::
computeConsistentTangentOperator(tfel::material::ThermalNorton<hypothesis, Type, false>::SMType)’:
ThermalNorton.mfront:147:75: error: ‘tum_2202__tum_0394__tum_03B5__eltum_2215__tum_2202__tum_0394__T’
was not declared in this scope

can be significantly improved by tfel-unicode-filt:

$ mfront --obuild  --interface=generic ThermalNorton.mfront 2>&1 | tfel-unicode-filt
Treating target : all
In file included from ThermalNorton-generic.cxx:33:0:
ThermalNorton.mfront: In member function ‘bool tfel::material::ThermalNorton<hypothesis, Type, false>::
computeConsistentTangentOperator(tfel::material::ThermalNorton<hypothesis, Type, false>::SMType)’:
ThermalNorton.mfront:147:75: error: ‘∂Δεel∕∂ΔT’ was not declared in this scope

8 Improvements to tfel-config

The command line option --debug-flags has been added to tfel-config. When used, tfel-config returns the standard debugging flags.

9 Improvements to the build system

9.1 Exporting CMake’ targets

9.2 Disabling NumPy support

10 Tickets solved during the development of this version

10.1 Ticket #250: Add a new inelastic flow to the StandardElastoViscoPlasticity brick

This ticket requested the addition of the HarmonicSumOfNortonHoffViscoplasticFlows inelastic flow. See Section 4.5.2 for details.

For more details, see: https://sourceforge.net/p/tfel/tickets/250/

10.2 Ticket #234: Import behaviour parameters in MTest

For more details, see: https://sourceforge.net/p/tfel/tickets/234/

10.3 Ticket #231: Support for tensors as gradients and thermodynamic forces in the generic behaviours

For more details, see: https://sourceforge.net/p/tfel/tickets/231/

10.4 Ticket #219: Add the possibility to define the tangent operator blocks

For more details, see: https://sourceforge.net/p/tfel/tickets/219/

10.5 Ticket #214: Add a debugging option to MFront

The -g option of MFront now adds standard debugging flags to the compiler flags when compiling shared libraries.

For more details, see: https://sourceforge.net/p/tfel/tickets/214/

10.6 Ticket #212: Better const correctness in the generic behaviour

The state at the beginning of the time step is now described in a structure called mfront::gb::InitialState, the fields of which are all const.

The following fields of the mfront::gb::State are now const:

• gradients
• material_properties
• external_state_variables

For more details, see: https://sourceforge.net/p/tfel/tickets/212/

10.7 Ticket #209: lack of documentation of the @GasEquationOfState keyword

This feature is now described in the (MTest page)[mtest.html]

For more details, see: https://sourceforge.net/p/tfel/tickets/209/

10.8 Ticket #206: Export TFEL targets for use by external projects

Here is a minimal example on how to use this feature:

project("tfel-test")
cmake_minimum_required(VERSION 3.0)

find_package(TFELException REQUIRED)
find_package(TFELMath REQUIRED)

add_executable(test-test test.cxx)
target_link_libraries(test-test tfel::TFELMath)

For more details, see: https://sourceforge.net/p/tfel/tickets/209/

10.9 Ticket #205: Add power isotropic hardening rule

This feature is described in Section 4.5.6.

For more details, see: https://sourceforge.net/p/tfel/tickets/205/

10.10 Ticket #201: Allow better control of the convergence in the StandardElastoviscoPlascity brick

See Sections 4.5.4.1 and 4.5.4.2.

For more details, see: https://sourceforge.net/p/tfel/tickets/201/

10.11 Ticket #200: Allow choosing the eigen solver for some stress criteria in the StandardElastoviscoPlascity brick

See 4.5.3.

For more details, see: https://sourceforge.net/p/tfel/tickets/200/

10.12 Ticket #195 : Export variables bounds for material properties

Variables bounds (both @Bounds and @PhysicalBounds) are now available for material properties. They are available directly in the .so file via getExternalLibraryManager().

For more details, see: https://sourceforge.net/p/tfel/tickets/195/

10.13 Ticket #202: DSLs for isotropic behaviours don’t handle NaN

The IsotropicMisesCreep, IsotropicMisesPlasticFlow, IsotropicStrainHardeningMisesCreep and MultipleIsotropicMisesFlowsDSL now handle properly NaN values.

For more details, see: https://sourceforge.net/p/tfel/tickets/202/

10.14 Ticket #196 : Export variable names for all interface of material property

The variable name of material property was available only for castem interface. Now it is available for all interface (c++, python, …). The name can be found in the .so file via getExternalLibraryManager().

For more details, see: https://sourceforge.net/p/tfel/tickets/196/

References