We present here an implementation of Ponte-Castaneda variational bound in non-linear elasticity [1]. It deals with the homogenization of a composite made of a matrix and spherical inclusions. The two phases have a non-linear elastic behaviour. The variational bound from Ponte-Castaneda is based on the computation of the strain second-moments.

This tutorial first recalls the scheme, and presents the implementation.

Ponte-Castaneda variational bound

The non-linear homogenization problem

The variational approach used by Ponte-Castaneda is based on the elastic potential \(w\) which is of the form: \[\begin{aligned} w(\underline{\varepsilon})= \sum_{r=1}^{N}\chi_r\,w_r (\underline{\varepsilon}) \end{aligned}\]

where \(N\) is the number of phases and \(\chi_r\) is characteristic function of phase \(r\).

The local potential \(w_r\) is a non-linear function of the strain \(\underline{\varepsilon}\), but here we focus on potentials of the form \[\begin{aligned} w_r(\underline{\varepsilon})={\displaystyle \frac{\displaystyle 9}{\displaystyle 2}} k_r\, \varepsilon_m^2+f_r (\varepsilon_{\mathrm{eq}}^2) \end{aligned}\] where \[\begin{aligned} \varepsilon_{\mathrm{eq}}= \sqrt{{\displaystyle \frac{\displaystyle 2}{\displaystyle 3}}\underline{\varepsilon}^d:\underline{\varepsilon}^d}\qquad\text{where}\quad \underline{\varepsilon}^d = \underline{\varepsilon}- {\displaystyle \frac{\displaystyle 1}{\displaystyle 3}} \mathrm{tr}\left(\underline{\varepsilon}\right)\underline{1} \qquad\text{and}\quad \varepsilon_m={\displaystyle \frac{\displaystyle 1}{\displaystyle 3}} \mathrm{tr}\left(\underline{\varepsilon}\right) \end{aligned}\] In the variational approach, the homogenization problem is equivalent to a minimization problem: \[\begin{aligned} \underline{\varepsilon}=\underset{\underline{\varepsilon}\in\mathcal K(\overline{\underline{\varepsilon}})}{\textrm{argmin}} \langle w(\underline{\varepsilon})\rangle \end{aligned}\]

where the space of kinematically admissible fields \(\mathcal K(\overline{\underline{\varepsilon}})\) is introduced depending on the boundary conditions used, and it makes intervene the loading \(\overline{\underline{\varepsilon}}\) (which will be our total strain \(\texttt{eto}\)). The \(\langle.\rangle\) denotes the average on the representative volume element.

The variational bound

Ponte-Castaneda’s idea is to use the dual function \(f_r^*\) of \(f_r\), under an hypothesis of concavity of \(f_r\). Note that \(w_r\) is convex relatively to \(\underline{\varepsilon}\), but the hypothesis is: \(f_r\) concave relatively to \(\varepsilon_{\mathrm{eq}}^2\), which adds a supplementary restriction to the behaviour. \[\begin{aligned} w_r(\underline{\varepsilon})=\underset{\mu_0^r(\underline{x})}{\min} \left\{{\displaystyle \frac{\displaystyle 9}{\displaystyle 2}} k_r\, \varepsilon_m^2+{\displaystyle \frac{\displaystyle 3}{\displaystyle 2}} \mu_0^r(\underline{x})\, \varepsilon_{\mathrm{eq}}^2-f_r^*(\dfrac32\mu_0^r(\underline{x}))\right\} \end{aligned}\] where the dual function \(f_r^*\) is defined as \[\begin{aligned} f_r^*(\lambda_0)=\underset{e}{\min} \left\{\lambda_0 e-f_r(e)\right\} \end{aligned}\] Considering uniform per phase shear moduli \(\mu_0^r\) (also called the ‘secant moduli’), and after a few manipulations, Ponte-Castaneda arrives at the following bound on the effective energy \(W^{\mathrm{eff}}(\overline{\underline{\varepsilon}})\): \[\begin{aligned} W^{\mathrm{eff}}(\overline{\underline{\varepsilon}})=\underset{\underline{\varepsilon}\in\mathcal K(\overline{\underline{\varepsilon}})}{\textrm{min}} \langle w(\underline{\varepsilon})\rangle \leq \overline{w}(\overline{\underline{\varepsilon}})=\underset{\mu_0^r}{\min} \left\{W_0^{\mathrm{eff}}(\overline{\underline{\varepsilon}})-\sum_r c_r\, f_r^*(\dfrac32\mu_0^r)\right\} \end{aligned}\]

where \(c_r\) is the volume fraction of phase \(r\) and \(W_0^{\mathrm{eff}}(\overline{\underline{\varepsilon}})\) is the effective energy relative to a ‘linear comparison composite’ which is heterogeneous, and whose elastic moduli are the \(k_r\) and the \(\mu_0^r\).

The stationarity conditions associated to the minimization on \(\mu_0^r\) are: \[\begin{aligned} {\displaystyle \frac{\displaystyle \partial W_0^{\mathrm{eff}}}{\displaystyle \partial \mu_0^r}} = \dfrac{3c_r}{2}\,\left(f_r^*\right)'(\dfrac32 \mu_0^r) \end{aligned}\] which can be shown to be equivalent to \[\begin{aligned} \mu_0^r= {\displaystyle \frac{\displaystyle 2}{\displaystyle 3}} f_r'\left(\langle \varepsilon_{\mathrm{eq}}^2\rangle_r\right) \end{aligned}\] where \(\varepsilon_{\mathrm{eq}}\) is relative to \(\underline{\varepsilon}\) solution of the homogenization problem: \[\begin{aligned} \mathrm{div}\left(3k_r\,\varepsilon_m\,\underline{1}+2\mu_0^r\,\underline{\varepsilon}^d\right)=0,\qquad\underline{\varepsilon}\in\mathcal K(\overline{\underline{\varepsilon}}) \end{aligned}\] Besides, noting that \[\begin{aligned} W_0^{\mathrm{eff}}(\overline{\underline{\varepsilon}})=\sum_r c_r\,\left({\displaystyle \frac{\displaystyle 9}{\displaystyle 2}} k_r\,\langle\varepsilon_m^2\rangle_r+{\displaystyle \frac{\displaystyle 3}{\displaystyle 2}} \mu_0^r\langle \varepsilon_{\mathrm{eq}}^2\rangle_r\right) \end{aligned}\] it follows that \[\begin{aligned} \langle \varepsilon_{\mathrm{eq}}^2\rangle_r= {\displaystyle \frac{\displaystyle 2}{\displaystyle 3c_r}}{\displaystyle \frac{\displaystyle \partial W_0^{\mathrm{eff}}}{\displaystyle \partial \mu_0^r}} \end{aligned}\]

Macroscopic stress and tangent operator

The macroscopic stress \(\overline{\underline{\sigma}}\) is also shown to be (see [2], eq. (4.41)): \[\begin{aligned} \overline{\underline{\sigma}}={\displaystyle \frac{\displaystyle \partial \overline{w}}{\displaystyle \partial \overline{\underline{\varepsilon}}}}={\displaystyle \frac{\displaystyle \partial W_0^{\mathrm{eff}}}{\displaystyle \partial \overline{\underline{\varepsilon}}}}=\underline{\mathbf{C}}_0^{\mathrm{eff}}:\overline{\underline{\varepsilon}} \end{aligned}\]

where \(\underline{\mathbf{C}}_0^{\mathrm{eff}}\) is the effective elasticity of the linear comparison composite. In our case, we use Hashin-Shtrikman bounds.

The tangent operator is given by \[\begin{aligned} \dfrac{\mathrm{d}\overline{\underline{\sigma}}}{\mathrm{d}\overline{\underline{\varepsilon}}}=\underline{\mathbf{C}}_0^{\mathrm{eff}}+\dfrac{\mathrm{d}\underline{\mathbf{C}}_0^{\mathrm{eff}}}{\mathrm{d}\overline{\underline{\varepsilon}}} \end{aligned}\]

Here, the derivative of \(\underline{\mathbf{C}}_0^{\mathrm{eff}}\) w.r.t. \(\overline{\underline{\varepsilon}}\) can be computed by derivating the Hashin-Shtrikman moduli w.r.t. the secant moduli \(\mu_0^r\) and the derivatives of these moduli w.r.t. \(\overline{\underline{\varepsilon}}\). However, it is tedious and in the implementation, we see that the convergence of the Newton Raphson algorithm is good if we only retain the first term \(\underline{\mathbf{C}}_0^{\mathrm{eff}}\) in the tangent operator.

Summary and possible implementations

The resolution hence consists in \[ \text{Find}\,e^r=\langle \varepsilon_{\mathrm{eq}}^2\rangle_r\,\text{such that}\quad\langle \varepsilon_{\mathrm{eq}}^2\rangle_r= {\displaystyle \frac{\displaystyle 2}{\displaystyle 3c_r}}{\displaystyle \frac{\displaystyle \partial W_0^{\mathrm{eff}}}{\displaystyle \partial \mu_0^r}} \] where \(W_0^{\mathrm{eff}}\) is the effective energy of a linear comparison composite whose elastic moduli are \(k_r\) annd \(\mu_0^r\) such that: \[ \mu_0^r= {\displaystyle \frac{\displaystyle 2}{\displaystyle 3}}{\displaystyle \frac{\displaystyle \partial f_r}{\displaystyle \partial e}}\left(\langle \varepsilon_{\mathrm{eq}}^2\rangle_r\right). \]

Possible implementations

The iterative resolution of the non-linear equation can be summarized as \[ \underset{\substack{\\ \\ \\ \Downarrow\\ \\ \\\text{analytic / finite difference}\\ \\ \\\text{\texttt{@BehaviourVariable} / directly provided}}}{\mu_0^r= {\displaystyle \frac{\displaystyle 2}{\displaystyle 3}}{\displaystyle \frac{\displaystyle \partial f_r}{\displaystyle \partial e}}\left(\langle \varepsilon_{\mathrm{eq}}^2\rangle_r\right)}\quad\rightarrow\quad \underset{\substack{\\ \\ \\ \Downarrow\\ \\ \\\text{mean-field scheme / morphological tensors}\\ \\ \\\texttt{tfel::material::homogenization}}}{W_0^{\mathrm{eff}}\left(\mu_0^r\right)= \dfrac12\overline{\underline{\varepsilon}}:\underline{\mathbf{C}}_0^{\mathrm{eff}}:\overline{\underline{\varepsilon}}}\quad\rightarrow\quad\underset{\substack{\\ \\ \\ \Downarrow\\ \\ \\\text{analytic / finite difference}\\ \\ \\\texttt{tfel::material::homogenization}}}{\langle \varepsilon_{\mathrm{eq}}^2\rangle_r= {\displaystyle \frac{\displaystyle 2}{\displaystyle 3c_r}}{\displaystyle \frac{\displaystyle \partial W_0^{\mathrm{eff}}}{\displaystyle \partial \mu_0^r}}} \]

And the macroscopic stress must also be computed: \[ \overline{\underline{\sigma}}=\underline{\mathbf{C}}_0^{\mathrm{eff}}:\overline{\underline{\varepsilon}} \]

The first step of the resolution consists in computing the secant modulus \(\mu_0^r\) and it can be done analytically (as below) or via finite difference or automatic differentiation. Moreover, for both strategies, we could use a BehaviourVariable, defining the function \(f_r\) in an external file (in our example, the function is to simple to do that).

The second step consists in computing the effective energy \(W_0^{\mathrm{eff}}\). This will be done via tfel::material::homogenization. This namespace provides classical mean-field schemes (we use a Hashin-Shtrikman bound in our example below). This could also be done with interaction tensors, providing externally. In another tutorial we show that we can take into account more specifically the morphology of a polycrystal by providing interaction tensors.

The third step consists in the computation of the second-moments. This is also done via tfel::material::homogenization. Here again, there are two strategies: analytical computation when possible, and finite difference or automatic differentiation when the analytical derivation is too tedious or even impossible. In our example below, the computation is analytic.

Implementation in MFront

Example used for the implementation

In the application of the implementation, we take the example of the following behaviour: \[\begin{aligned} w_r(\underline{\varepsilon})=\dfrac{9}{2}k_r\,\varepsilon_{m}^2+\dfrac{\sigma_r^0}{n+1}\,\varepsilon_{eq}^{n+1} \end{aligned}\]

where \(n\) is between \(0\) and \(1\), which means that \(f_r(e)=\dfrac{\sigma_r^0}{n+1}\,e^{\frac{n+1}2}\) (note that the function \(f_r\) is effectively concave relatively to \(e\), because \(0\lt n\leq 1\)).

Moreover, we make the choice of purely elastic inclusions. Hence, only the matrix is non-linear and has a secant modulus.

The unknowns of our non-linear problem are the \(e^r\). The secant moduli \(\mu_0^r\) can be computed by derivation of the function \(f_r\) which is given by the behaviour. In the precise case detailed above, we have \[\begin{aligned} {\displaystyle \frac{\displaystyle \partial f_r}{\displaystyle \partial e}}(e)=\dfrac{\sigma_r^0}{2}\,e^{\frac{n-1}2}\qquad\text{and}\quad\mu_0^r=\dfrac{\sigma_r^0}{3}\,\left(e^r\right)^{\frac{n-1}2} \end{aligned}\] Then, the effective energy of the linear comparison composite can be computed via a mean-field scheme. In our implementation, we proposed to use the Hashin-Shtrikman bound. The \(e^r\) must then cancel the following residue: \[\begin{aligned} r_{e^r}=e^r - {\displaystyle \frac{\displaystyle 2}{\displaystyle 3\,c_r}}{\displaystyle \frac{\displaystyle \partial W_0^{\mathrm{eff}}}{\displaystyle \partial \mu_0^r}} \end{aligned}\]

which means that we only need the derivative of the Hashin-Shtrikman bound. This will be given by the tfel::material::homogenization functionalities.

Details of implementation

The file PonteCastaneda1992.mfront is available in the MFrontGallery project, here.

For the jacobian, we adopt the Numerical Jacobian, which means that the beginning of the mfront file reads:

@DSL ImplicitII;
@Behaviour PC_VB_92;
@Author Martin Antoine;
@Date 12 / 12 / 25;
@Description{"Ponte Castaneda variational bounds for homogenization of non-linear elasticity (one potential), based on second-moments computation"};
@UseQt true;
@Algorithm NewtonRaphson_NumericalJacobian;
@PerturbationValueForNumericalJacobianComputation 1e-10;
@Epsilon 1e-12;

Moreover, the following libraries will be needed for computation of the stress and secant modulus:

@TFELLibraries {"Material"};
@Includes{
#include "TFEL/Material/IsotropicModuli.hxx"
#include "TFEL/Material/HomogenizationSecondMoments.hxx"
#include "TFEL/Material/LinearHomogenizationBounds.hxx"
}

We define two state variables which are the averages (on each phase) of the squares of the equivalent strains, and correspond to the \(e^r\):

@StateVariable real e_0;
e_0.setEntryName("MatrixSquaredEquivalentStrain");
@StateVariable real e_r;
e_r.setEntryName("InclusionSquaredEquivalentStrain");

The secant moduli are computed by derivation of function \(f_r\), which is detailed above. Hence

@Integrator {
//secant modulus/////////////////////////////////
const auto po = std::pow(max(e_0+de_0,real(1e-10)),0.5*(n_-1));
const auto mu0 = sig0/3.*po;

The second moment is given by the function computeMeanSquaredEquivalentStrain (see documentation):

//second moments/////////////////////////////////
const auto em = tfel::math::trace(eto+deto)/3.;
const auto ed = tfel::math::deviator(eto+deto);
const auto em2 = em*em;
const auto eeq2 = 2./3.*(ed|ed);
using namespace tfel::material;
const auto kg0 = KGModuli<stress>(k_m,mu0);
const auto kgr = KGModuli<stress>(kar,mur);
using namespace tfel::material::homogenization::elasticity;
const auto eeq2_ = computeMeanSquaredEquivalentStrain(kg0,fr,kgr,em2,eeq2);
const auto eeq20=std::get<0>(eeq2_);
const auto eeq2r=std::get<1>(eeq2_);

Now we can write the residues:

//residues/////////////////////////////////////
fe_0 = e_0+de_0 - eeq20;
fe_r = e_r+de_r - eeq2r;

There is no jacobian because we use the NumericalJacobian. The macroscopic stress is given by the Hashin-Shtrikman lower bound (indeed, the lower bound is better suited for soft matrix and rigid inclusions):

//sigma//////////////////////////////////////
vector<real> tab_f={1-fr,fr};
vector<stress> tab_k = {k_m,kar};
vector<stress> tab_mu = {mu0,mur};
const auto HSB=computeIsotropicHashinShtrikmanBounds<3,stress>(tab_f,tab_k,tab_mu);
const auto LB=std::get<0>(HSB);
const auto kHS=std::get<0>(LB);
const auto muHS=std::get<1>(LB);
Chom=3*kHS*J+2*muHS*K;
sig = Chom*(eto+deto);
}

(Note that Chom is the effective elastic tensor, defined here as a local variable). Afterwards, we can give the tangent operator:

@TangentOperator{
Dt=Chom;
}

Results

We then use MTest to simulate a strain-imposed test.

MTest file is the following:

@ModellingHypothesis 'Tridimensional';
@Behaviour<Generic> 'src/libBehaviour.so' 'PC_VB_92';
@ExternalStateVariable 'Temperature' {0 : 1000,1:1000};

@MaterialProperty<constant> 'sig0'             1.e9;
@MaterialProperty<constant> 'n_'               0.05;
@MaterialProperty<constant> 'k_m'               1.e9;
@MaterialProperty<constant> 'kar'               1.e15;
@MaterialProperty<constant> 'mur'               1.e15;
@MaterialProperty<constant> 'fr'               0.25;

@ImposedStrain 'EXX' {0 : 0, 100 : 0.8660254};
@ImposedStrain 'EYY' {0 : 0, 100 : -0.8660254};
@ImposedStrain 'EZZ' {0 : 0, 100 : 0};
@ImposedStrain 'EXY' {0 : 0, 100 : 0};
@ImposedStrain 'EXZ' {0 : 0, 100 : 0};
@ImposedStrain 'EYZ' {0 : 0, 100 : 0};
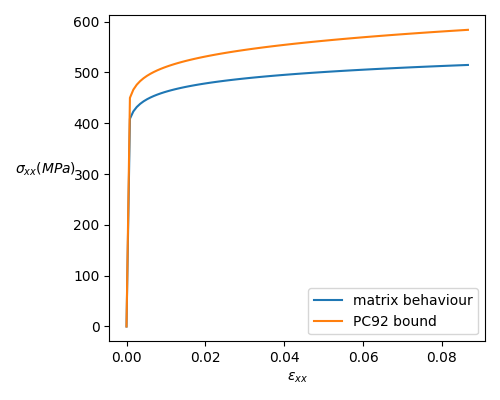
@Times {0.,10 in 100};

The macroscopic stress \(\sigma_{xx}\) is represented below as a function of the macroscopic strain \(\varepsilon_{xx}\):

Macroscopic stress as function of the macroscopic strain

We also plotted the behaviour of the matrix when there is no inclusions (it gives an idea of the reinforcement given by the inclusions).

1.
Castañeda, P.Ponte. New variational principles in plasticity and their application to composite materials. Journal of the Mechanics and Physics of Solids. November 1992. Vol. 40, no. 8, p. 1757–1788. DOI 10.1016/0022-5096(92)90050-C. Available from: https://linkinghub.elsevier.com/retrieve/pii/002250969290050C
2.
Ponte Castaneda, Pedro and Suquet, Pierre. Nonlinear composites. 1998. Advances in Applied Mechanics. ISBN 978-0-12-002034-8.