
Norton.mfrontMFront and
Salome-MECALa siguiente página es una introducción a MFront / MTest 2.0.4 y Salome-Meca 2016.
Te da una buena visión general de las habilidades de MFront y MTest y todos los ejemplos funcionarán con las versiones más recientes. Sin embargo, las nuevas versiones (>= 3.0.x) introducen nuevos conceptos e instrucciones que simplifican aún más la implementación de nuevos comportamientos mecánicos (en particular, el bloque StandardElasticity descrito aquí.
MFront es un generador de código dedicado al
conocimiento del material. A partir de un archivo que contiene la
información física y numérica, mfront genera uno o más archivos C++
utilizables en distintos programas.
El conocimiento del material viene cubierto por tres partes:
Para ofrecer una solución adaptada a diferentes situaciones, este generador de código es compatible con varios programas de análisis. Hay diferentes interfaces disponibles para adaptar el código generado al software de destino.
Se proporcionan varias interfaces para los solucionadores de elementos finitos:
Cast3MCode AsterAbaqus StandardAbaqus ExplicitZebulonY para los solucionadores de transformada rápida de Fourier
TMFFT y AMITEX_FFTP desarrollados internamente
en CEA.
Para las propiedades de los materiales, también se proporcionan
varias interfaces y cubren los siguientes lenguajes: C,
C++, Python, Fortran, etc.
Para poder hacernos a la idea de cómo funciona MFront, empezaremos con un ejemplo práctico de la implementación de la ley de comportamiento de Norton.
Teniendo en cuenta que el objetivo de esta guía es el funcionamiento de MFront y no el propio entendimiento del comportamiento de los materiales o de las leyes como la que se describe en este punto, no se entrará en más detalle que el necesario en lo que no se refiera al propio programa.
Así que, a modo de resumen, la ley de Norton es una ley de comportamiento viscoplástica, es decir, una ley que estipula que el comportamiento de deformación permanente de un material depende de la intensidad y la velocidad de carga.
Esta ley viene definida por:
\[ \left\{ \begin{array} \underline{\epsilon}^{\mathrm{to}}\underline{\epsilon}^{\mathrm{to}}&= \underline{\epsilon}^{\mathrm{el}}+ \underline{\epsilon}^{\mathrm{vis}}\\ \underline{\sigma}&= \underline{\mathbf{D}} :\ \underline{\epsilon}^{\mathrm{el}}\\ \underline{\epsilon}^{\mathrm{vis}}&= \dot{p} \\ \dot{p} &= A\sigma_{\text{eq}}^{m} \\ \end{array} \right. \]
Donde \(\underline{\mathbf{D}}\) viene calculado a partir del modulo de Young \(E\) y del coeficiente de Poisson \(\nu\).
Sin entrar en detalle sobre la función de cada variable, para integrar esta ley en un cálculo de estructura, se debe discretizar en el tiempo definiendo una sucesión de instantes de calculo \({\{ t_{i}\}}_{1 \leq i \leq I}\) y reemplazando las derivadas respecto el tiempo por los incrementos en el intervalo \(t = t_{i} - t_{i - 1}\):
\[ \left\{ \begin{aligned} \Delta\,\underline{\epsilon}^{\mathrm{el}}- \Delta\,\underline{\epsilon}^{\mathrm{to}}+ \Delta\,p\,\underline{n} = 0 \\ \Delta\,p - \Delta\,t\, A\,\sigma_{\mathrm{eq}}^{m} = 0 \end{aligned} \right. \]
Donde se obtiene un sistema de 7 ecuaciones: 6 ecuaciones relativas a la descomposición aditiva de la deformación de los tensores (en 3D), y una ecuación relativa al flujo visco-plastico. Las 7 incógnitas son las 6 componentes de \(\underline{\epsilon}^{\mathrm{el}}\) y \(p\).
La resolución implícita del sistema se hace por un método de Newton.
A continuación, en la Ilustración 1, se muestra un ejemplo de la
implantación del resultado obtenido de la resolución implícita del punto
anterior a un archivo MFront, donde tan solo se necesita escribir el
siguiente código con un editor de texto sin formato y guardar-lo con
extensión ..mfront.

Un fichero mfront empieza normalmente por una parte
descriptiva indicando el algoritmo utilizado para la resolución, el
nombre del comportamiento (en este caso Norton), y a continuación la
lista de materiales utilizados, la definición de las variables internas
y finalmente la descripción de las ecuaciones del sistema a
resolver.
@Parser: indica el método de integración que se
utilizará.@Behaviour: da el nombre del comportamiento.@Algorithm NewtonRaphson_NumericalJacobian: informa del
algoritmo utilizado.@RequireStiffnessTensor: solicita el cálculo de la
matriz de elasticidad. Esto generalmente indica que algunas propiedades
de material extra serán introducidas y manejadas por la interfaz antes
de la integración del comportamiento.@MaterialProperty: define las propiedades del material
de la ley.@StateVariable: declara la variable interna p.@ComputeStress: introduce un bloque de código destinado
a calcular el tensor simétrico de tensión.@Integrator: define las ecuaciones a resolver.@TangentOperator: introduce un bloque de código
utilizado para definir el operador tangente. Este código se llama una
vez que se han actualizado las variables de integración, las tensiones y
las variables de estado auxiliares.Una vez creado el archivo con la extensión .mfront se
puede al fin compilar accediendo a su ubicación a través del
Terminal y con la siguiente línea de comandos:
$ mfront --obuild --interface=aster Norton.mfrontDefiniendo en el parámetro --interface el código que se
desea utilizar, correspondiendo la interface aster a
Code_Aster.
Esto genera dos directorios: include y src
con varios archivos en cada uno, particularmente, en el directorio
src se generan las librerías dinámicas:
src/libAsterBehaviour.so
MTestLa utilidad MTest incluida en el paquete TFEL/MFront
permite efectuar simulaciones para calcular la respuesta a las tensiones
o deformaciones.
Para ello debemos crear un archivo con extensión .mtest
como el que se muestra a continuación en la Ilustración 2:

@Behaviour: declara el comportamiento utilizado para la
prueba. Se indica la interfaz utilizada por el comportamiento.@MaterialProperty: define una propiedad de material. En
este caso @ExternalStateVariable: permite al usuario especificar
la evolución de las variables de estado externas, en este caso la
temperatura.@ImposedStress: permite al usuario imponer la evolución
de un componente de las tensiones.@Times: permite al usuario especificar una lista de
tiempos utilizados para los cálculos.Con el archivo Norton.mtest ya preparado, se puede
ejecutar la simulación a través del Terminal con la
siguiente línea de comandos:
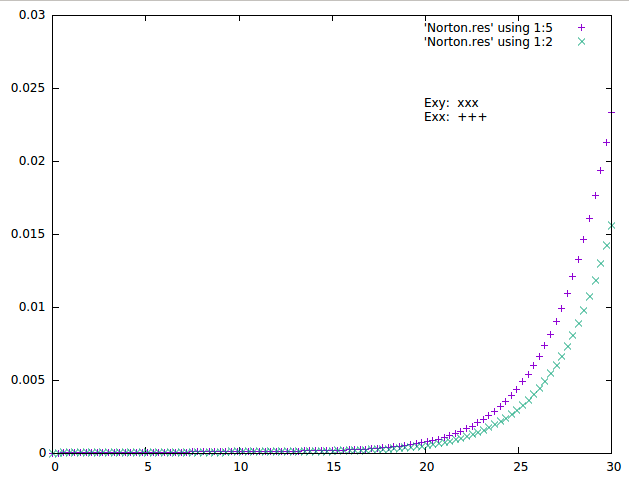
$ mtest Norton.mtestEsto generará un archivo Norton.res con el resultado
numérico de la simulación el cual se puede representar gráficamente con,
por ejemplo, gnuplot, dando un resultado como el de la
Ilustración 3:
Tal y como se ha visto, la creación de los archivos de entrada en
formato .mfront consisten en la edición de un archivo de
texto sin formato en el que se debe definir cada parte del código con
una serie de instrucciones señalizadas con @.
A lo largo de este apartado se describirán las instrucciones y parámetros de este archivo según su función.
Un archivo de entrada .mfront representa un único
conocimiento de material, es decir, una propiedad material, una ley de
comportamiento, o un modelo.
Este archivo de entrada se presenta como una lista de palabras clave,
o instrucciones, empezando con el símbolo @. Algunas partes
del archivo están directamente escritas en C++, pues MFront
se basa en este lenguaje, aunque intenta reducir al mínimo su uso para
hacerlo más accesible a las personas con menos capacidad de desarrollo
informático.
Orden de las instrucciones: No se impone un orden en las instrucciones, aunque se debe destacar que MFront analiza el archivo secuencialmente, por lo que no permitirá el uso de una variable antes de ser declarada. Por ejemplo, será imposible especificar el rango de validez de la temperatura de una propiedad del material antes de declarar que dicha propiedad depende de la temperatura.
Comentarios: MFront acepta los dos tipos de comentarios de C++, es decir, los que empiezan por /* y terminan por */ pudiendo estos ocupar varias líneas, y los que empiezan por // extendiéndose estos tan solo hasta el final de la línea actual.
El conocimiento de materiales soportado por MFront está clasificado en tres categorías:
Las propiedades de los materiales.
Los modelos.
Las leyes de comportamiento mecánico.
Para tratar estos conocimientos, hay disponibles diferentes analizadores:
DefaultParser, DefaultCZMParser,
DefaultFiniteStrainParser: Estos analizadores son los más
genéricos ya que no hacen ninguna restricción sobre el comportamiento o
el método de integración que se puede utilizar.Implicit: Este analizador proporciona un integrador
genérico basado en un esquema implícito. La deformación elástica no se
define automáticamente com una variable de estado.ImplicitII: Este analizador proporciona un integrador
genérico basado en un método theta. A diferencia de
Implicit, la deformación elástica no se define
automáticamente como una variable de estado.ImplicitFiniteStrain: Este analizador proporciona un
integrador genérico basado en un método theta.IsotropicMisesCreep: Este analizador se usa para los
comportamientos de flujo estándar de la forma \(\dot{p} = f(s)\) donde p es la
deformación equivalente y s la tensión equivalente.IsotropicPlasticMisesFlow: Este analizador se usa para
los comportamientos de plásticos estándar con superficie de rendimiento
de la forma \(f\left( s,p \right) =
0\).IsotropicStrainHardeningMisesCreep: Este analizador se
usa para los comportamientos de flujo de endurecimiento por deformación
estándar de la forma \(\dot{p} =
f(s,p)\).MultipleIsotropicMisesFlows: Este analizador se usa
para definir comportamientos combinando varios flujos isotrópicos. Los
tipos de flujos soportados son ‘Creep’(\(\dot{p} = f(s)\)),
’StrainHardeningCreep’ (\(\dot{p} =
f(s,p)\)) y ‘Plasticity’ (\(f\left( s,p \right) = 0\)).RungeKutta: Este analizador proporciona un integrador
genérico basado en uno de los muchos algoritmos Runge-Kutta.MaterialLaw: Este analizador se usa para definir las
propiedades del material.Model: Este analizador se usa para definir modelos de
materiales simples.La instrucción @Parser define el analizador con el que
se trabajará, el cual tiene su propio conjunto de instrucciones
admitidas, es decir, cada analizador admite ciertas instrucciones.
@Parser MaterialLaw;Todas las instrucciones disponibles en MFront están clasificadas según los analizadores que las pueden usar en el “Anexo 1 – Instrucciones Disponibles”.
A continuación, se describen algunas de las instrucciones más comunes.
En este punto se describirán cuatro instrucciones opcionales cuyo objetivo es tan solo informativo.
@Author se usa para dar el nombre de quien ha escrito el
archivo mfront.
@Author Jordi Alberich;@Description describe la propiedad del material, el
comportamiento o el modelo que se implementa en el archivo.
@Description{
Aquí se suelen describir las referencias del artículo o informe técnico
del que se extrae la propiedad del material, el comportamiento o el
modelo.
El nombre de los autores.
Las modificaciones hechas.
}@Date permite al usuario especificar cuándo se escribió
el archivo mfront.
@Date 2016-11-23;@Material permite al usuario especificar qué material es
tratado por el archivo actual.
@Material UO2;Para minimizar errores, con la instrucción @MaterialLaw
MFront permite importar la definición de una ley material definida en un
archivo mfront y compila, como parte de la biblioteca actual, una
función utilizando la interfaz mfront.
Los archivos a importar se buscarán en este orden:
--search-path o --include.MFRONT_INCLUDE_PATH.Como ejemplo, si se ha definido en un archivo:
@Parser MaterialLaw;
@Law ThermalExCoef;
@Material AE1307Inventado;
@Author Jordi Alberich;
//… … …Este se podrá usar en otro con la instrucción
@MaterialLaw:
@MaterialLaw "AE1307Inventado_ThermalExCoef.mfront";
@InitiLocalVariables {
a = AE1307Inventado_ThermalExCoef(T+theta\*dT);
}Por otra parte, la instrucción @Import permite la
inclusión de uno o varios archivos mfront externos.
Esta instrucción interrumpe el tratamiento del archivo actual e inicia el tratamiento secuencial de cada archivo a importar.
El orden de las rutas de búsqueda del archivo a importar será el
mismo que en el caso de @MaterialLaw.
@Import "SlidingSystemsCC.mfront";Hay tres instrucciones relacionadas con la compilación de fuentes.
Las instrucciones @Include y @Link tienen una
importancia particular debido a que permiten utilizar características
definidas en librerías C++ externas.
@Library permite al usuario especificar el nombre de la
librería generada.
@Library LibreriaJordi;@Includes presenta un bloque donde el usuario puede
definir algunas instrucciones del preprocesador C++, normalmente
instrucciones del tipo #include.
@Includes{
#include<fstream>
#include<TFEL/Material/Lame.hxx>
}@Link se usa para vincular librerías generadas con
librerías externas.
//link explicito con libm.so
@Link "-lm";Hay variables de estado que pueden tener límites inherentes, como por ejemplo, una temperatura no puede ser negativa, o una porosidad superior a 1.
Para gestionar estos límites, se ofrecen estas instrucciones:
@Bounds que permite al usuario definir el dominio de
validez.
Si la variable se encuentra fuera de sus límites, la mayoría de las interfaces permiten al usuario elegir una de las siguientes políticas:
None, que significa que no hace nada.Warning, que muestra un mensaje, pero los cálculos no
se detienen.Strict, que se detienen los cálculos con un mensaje de
error.// El intervalo puede contener el infinito, representado por el carácter '\*'.
@Bounds T in [293.15:873.15];@PhysicalBounds permite al usuario definir el dominio
físico de una variable. En los esquemas implícitos, si se establecen
límites físicos en una variable, esta variable se limita a satisfacerlos
durante las iteraciones internas.
Si se encuentra que una variable está fuera de sus límites físicos, los cálculos se detienen. Las pruebas se realizan en diferentes etapas de integración dependiendo de la naturaleza de la variable.
// La temperatura (en Kelvin) no puede ser negativa.
@PhysicalBounds T in [0:*[;Para la definición de parámetros para las propiedades y leyes de comportamiento, se han definido las siguientes instrucciones:
@Parameter declara un nuevo parámetro o una lista de
nuevos parámetros. Opcionalmente, el valor predeterminado de los
parámetros declarados también se puede dar siguiendo varias sintaxis de
asignación estándar de C++.
El valor predeterminado de un parámetro también se puede asignar después de su declaración utilizando la orden setDefaultValue.
@Parameter R0 = 500;
@Parameter Q1{10000},b1{0.00001};
@Parameter Q2(0),b2(0);
@Parameter fc;
fc.setDefaultValue(1.e-2);Para el analizador Model unas instrucciones específicas,
@GlobalParameter para definir los parámetros del modelo que
se podrán usar en otros modelos, y @LocalParameter para
definir parámetros especializados del modelo actual.
@GlobalParameter real a;
a.setDefaultValue(1.23);
@LocalParameter real b;
b.setDefaultValue(1.23);@FunctionLa instrucción @Function se usa en el analizador
MaterialLaw y permite definir en código C++ la propiedad
del material.
La salida predeterminada se denomina res, aunque se
puede cambiar con la instrucción @Output.
Aunque la mayoría de interfaces usan el double para las
operaciones con punto flotante, esto puede no ser siempre necesario. Se
ha introducido un typedef especial llamado
real recomendado para definir las variables locales.
@Function{
const real C0 = 575.57;
const real C1 = -21094.;
Cp = C0+C1/T;
}Las propiedades del material son uno de los elementos esenciales para el conocimiento del material. Una propiedad del material es una función de un conjunto de variables de estado termodinámico del material.
A continuación, se describirán los diferentes tipos de variables al
escribir las propiedades del material a usar con el analizador
MaterialLaw.
Las variables de entrada de las propiedades del material se definen
con la instrucción @Input.
Se recomienda asociar a una variable de entrada un glosario o nombre de entrada con la orden setGlossaryName.
@Input T,p;
T.setGlossaryName("Temperature");
p.setGlossaryName("Porosity");Tal como ya se ha descrito en el punto “La instrucción
@Function, la instrucción @Output permite
cambiar el nombre de la variable de salida que por defecto es
res.
@Output b;La instrucción @StaticVariable permite al usuario
definir un valor constante. A diferencia de los parámetros definidos con
@Parameter, los valores de las variables estáticas no se
pueden cambiar después de la compilación.
Al definir este tipo de variable, se deberá indicar el tipo de constante y su valor.
@StaticVariable real A = 1.234e56;La instrucción @Parameter ya se ha descrito en el punto
“Definición de parámetros”.
La instrucción @Constant permite al usuario definir un
valor constante. Esta instrucción es sinónima de la instrucción
@StaticVariable para una variable real.
@Constant A 1.234e56;Generalmente, se pueden distinguir dos tipos de modelos:
MFront no procesa los modelos que requieren de una solución global, tan solo puede tratar los modelos tipo “point”.
Para tratar estos modelos, MFront ofrece el analizador Model.
@ModelEste analizador no ofrece muchas instrucciones, y la mayoría de ellas
ya se han descrito en los puntos anteriores. Una de las únicas
instrucciones que se puede encontrar de más es la instrucción
@Model que tan solo permite al usuario definir el nombre
del modelo.
@Model SolidSwelling;Para el debido conocimiento del material, otro factor a tener en cuenta, sino quizás el más importante, es su comportamiento mecánico.
Los analizadores disponibles para definir los comportamientos mecánicos son:
DefaultParserDefaultCZMParserDefaultFiniteStrainParserIsotropicMisesCreepIsotropicPlasticMisesFlowIsotropicStrainHardeningMisesCreepMultipleIsotropicMisesFlowsRungeKuttaImplicitImplicitIIImplicitFiniteStrainComo se puede prever, el estudio de los comportamientos mecánicos podría llegar a ser muy extenso, y teniendo en cuenta que lo que se busca aprender en este trabajo es el uso de MFront, tan solo se describirán algunas de las instrucciones y funciones (no vistas en los puntos anteriores) sin entrar en demasiado detalle como qué métodos o analizadores usar y porqué.
@Algorithm se usa para seleccionar el algoritmo
numérico. Esta instrucción está disponible en los analizadores
Implícitos y Runge-Kutta.
Los algoritmos disponibles para los analizadores Implícitos son:
NewtonRaphsonNewtonRaphson_NumericalJacobianPowellDogLeg_NewtonRaphsonPowellDogLeg_NewtonRaphson_NumericalJacobianBroydenBroyden2PowellDogLeg_BroydenLevenbergMarquardtLevenbergMarquardt_NumericalJacobianY los algoritmos disponibles para el analizador
Runge-Kutta son: Euler, rk2,
rk4, rk42, rk54 y
rkCastem.
//Ejemplo en dsl Implicito
@Algorithm NewtonRaphson;//Ejemplo en dsl Runge-Kutta
@Algorithm rk54;@ModellingHypotheses permite especificar las hipótesis
de modelado. Las hipótesis válidas serán las siguientes:
AxisymmetricalGeneralisedPlaneStrainAxisymmetricalPlaneStressPlaneStrainGeneralisedPlaneStrainTridimensional@OrthotropicBehaviour declara que el material es
ortótropo, es decir, que tiene dos o tres ejes ortogonales entre sí, de
doble simetría rotacional, de forma que sus propiedades mecánicas son,
en general, diferentes en las direcciones de cada uno de esos ejes.
@OrthotropicBehaviour;@IsotropicElasticBehaviour declara que el comportamiento
elástico es isotrópico incluso si el material ha sido declarado
ortótropo. Esta declaración afecta al comportamiento
@RequireStiffnessTensor.
@IsotropicElasticBehaviour;@RequireStiffnessTensor requiere que el código calcule
la rigidez del tensor. Esto generalmente significa que se introducirán
algunas propiedades de material extra y serán usadas por la interfaz
antes de la integración del comportamiento.
@RequireStiffnessTensor true;@RequireThermalExpansionCoefficientTensor requiere que
el código calcule el tensor del coeficiente de expansión térmica.
@RequireThermalExpansionCoefficientTensor true;@MaterialProperty permite al usuario una varias
propiedades del material. Se le debe especificar el tipo de propiedad
del material y una lista de los nombres de las propiedades. Se
recomienda asociar a una propiedad del material un glosario o nombre con
las ordenes setGlossaryName o setEntryName.
@MaterialProperty stress young;
young.setGlossaryName("YoungModulus");@Sources permite al usuario definir un bloque de código
que se integrará a las fuentes generadas de un comportamiento. Esto
permite al usuario implementar sus propias clases o funciones. Estas
declaraciones de tales clases o funciones pueden realizarse en un bloque
de código introducido por la instrucción @Includes.
@Includes{
void f(void); //declaración de la función f
}@Sources{
void f(void){
std::cout << "Ejemplo de una función" << std::endl;
}
}@TangentOperator introduce un bloque de código utilizado
para definir el operador tangente. Este código se llama una vez que se
han actualizado las variables de integración, las tensiones y las
variables de estado auxiliares.
El tipo de operador tangente solicitado está dado por la variable smt
(Stiffness matrix type), cuyos posibles valores serán
ELASTIC, SECANT, TANGENTOPERATOR
y CONSISTENTTANGENTOPERATOR.
@TangentOperator{
if((smt==ELASTIC)||(smt==SECANTOPERATOR)){
Dt = 0;
} else if (smt==CONSISTENTTANGENTOPERATOR){
Dt = De * Je;
} else {
return false;
}
}@UpdateAuxiliaryStateVariables introduce un bloque de
código destinado a actualizar las variables de estado auxiliares después
de la integración.
En los lenguajes específicos de dominio implícito, el código
declarado por @UpdateAuxiliaryStateVariables se llama una
vez que se han actualizado las variables de integración (incluidas las
variables de estado) y las tensiones. Las variables de estado externas
no se actualizan.
En los lenguajes específicos de Runge-Kutta, el código declarado por
@UpdateAuxiliaryStateVariables se llama después de cada
paso de tiempo exitoso. Hay que tener en cuenta que la mayoría de
algoritmos de Runge-Kutta realiza subescalas internas, en este caso, el
código declarado por @UpdateAuxiliaryStateVariables puede
ser llamado varias veces durante la integración del comportamiento. Una
variable adicional llamada dt_, que es menor que el incremento de paso
de tiempo total dt si se realizan subpasos, da el
incremento de tiempo actual.
//Ejemplo dsl Implícito
@UpdateAuxiliaryStateVariables{
const real q_ = q–(1 – theta)*dq;
const real Q = Q0+(Qm–Q0)*(1–exp (-2*Mu*q_));
R+=b*(Q-R)*dp;
}//Ejemplo dsl Runge-Kutta
@UpdateAuxiliaryStateVariables{
sigeq = sqrt(sig|sig};
}@MaximumNumberOfIterations le permite al usuario definir
el número máximo de iteraciones.
@MaximumNumberOfIteration 200;@Theta se usa para definir el valor predeterminado del
parámetro \(\theta\) usado por los
esquemas implícitos. Si no se usa esta instrucción, los lenguajes de
dominio implícito le asignan su propio valor predeterminado (0.5 o
1).
El valor de \(\theta\) debe estar entre el rango ( ]0:1] ).
El valor de \(\theta\) se puede
cambiar durante la ejecución modificando el parámetro
theta.
@Theta 0.5;@Epsilon permite al usuario definir el valor del
criterio de convergencia.
Este valor se puede cambiar durante la ejecución modificando el
parámetro epsilon.
@Epsilon 1.e-12;@ComputeStress introduce un bloque de código destinado a
calcular el tensor simétrico de tensión. Esta instrucción interpreta el
código para generar dos métodos:
@ComputeFinalStress.Si el usuario proporciona una forma de calcular el estrés al final
del paso con la instrucción @ComputeFinalStress, se
considerará que el uso de @ComputeStress no tiene sentido y
aconseja al usuario calcular de forma explícita el esfuerzo como parte
del paso de integración.
@ComputeStress{
sig = (1-d)*(lambda*trace(eel)*Stensor::Id()+2*mu*eel);
}En este apartado se describirá como usar MFront en línea de comandos
una vez ya elaborado el archivo .mfront.
La forma genérica de uso de MFront es la siguiente:
$ mfront [opciones] [archivos]Las opciones disponibles para usar en línea de comandos con MFront son las siguientes:
--analyser: permite al usuario especificar el
analizador a utilizar.--build: genera el MakeFile y construye
las librerías.--clean: genera el MakeFile y limpia las
librerías.--debug: establece el modo de depuración (elimina las
referencias al archivo inicial)--help: muestra las opciones disponibles. También se
puede usar –h.--help-command y –help-keyword muestran la
ayuda asociada a la instrucción dada según el analizador indicado como
se puede ver en la Ilustración 4.
--help-commands-list y –help-keywords-list
muestran una lista de las instrucciones disponibles según el analizador
dado tal como se muestra en la Ilustración 5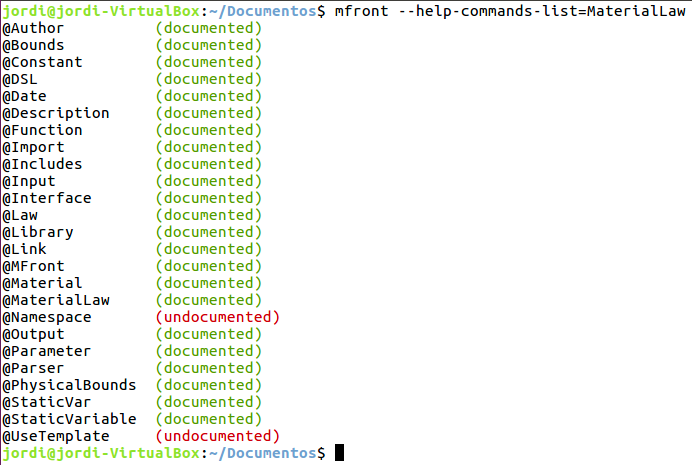
--include: y –search-path añaden una
nueva ruta al principio de las rutas de búsqueda. También se puede usar
como –I.--interface: especifica la interfaz a usar.--list-parsers: muestra una lista de los analizadores
disponibles añadiendo también una pequeña descripción de ellos como la
descrita en el punto “Uso de las instrucciones”.--make: genera el archivo
Makefile.mfront.-nodeps evita la inclusión de reglas de dependencia en
el archivo generado Makefile.mfront. Esta opción fue
introducida para evitar algunos problemas en Windows.--nomelt: evita fusionar directorios de librerías.--obuild, --omake genera el archivo
Makefile con compilaciones optimizadas y crea las
librerías. También se puede usar como –b o
–m.--otarget: permite compilar solo las librerías de
manera optimizada.--silent-build: activa o desactiva esta opción para
desplegar las líneas de compilación utilizadas.--target: permite compilar solo las librerías. También
se puede usar como –t.--verbose: establece el nivel de verbosidad pudiendo
ser:
quiet establece el nivel mínimo.level1, level2 y level3
establece los niveles crecientes.debug y full son generalmente para desarrollo.--version: muestra la versión instalada. También se
puede usar como –v.--warning: imprime los avisos. También se puede usar
como –W.--win32: permite la compilación de las librerías
dinámicas para un sistema Windows.MTest es una herramienta de simulación del
comportamiento mecánico de un punto material.
Con esta herramienta, el usuario puede simular varios ensayos mecánicos simples, por ejemplo:
Los resultados obtenidos se pueden comparar con las soluciones analíticas o soluciones de referencia. En la salida, se crean dos archivos:
La forma genérica de uso de MTest es la siguiente:
$ mtest [opciones] [archivos]Siendo las siguientes opciones disponibles:
--backtrace: pila del proceso de impresión al obtener
las señales SIGSEGV (error de segmentación) o
SIGFPE (excepción matemática). También se puede usar
–bt.--floating-point-exceptions: controla las excepciones
de punto flotante a través de las señales SIGFPE. También se puede usar
como –fpe.--help: muestra las opciones disponibles. También se
puede usar como –h.--help-command y --help-keyword: muestran
la ayuda asociada a la instrucción dada.--help-commands-list y
--help-keywords-list: muestran una lista de las
instrucciones disponibles tal y como se puede ver en la Ilustración
6.--residual-file-output: control de salida residual
(‘No’ por defecto).--result-file-output: control de la salida del
resultado (‘Si’ por defecto).--verbose: establece el nivel de verbosidad pudiendo
ser:
quiet establece el nivel mínimo.level1, level2 y level3
establece los niveles crecientes.debug y full son generalmente para desarrollo.--version: muestra la versión instalada. También se
puede usar como –v.--xml-output: salida xml de control (‘No’ por
defecto).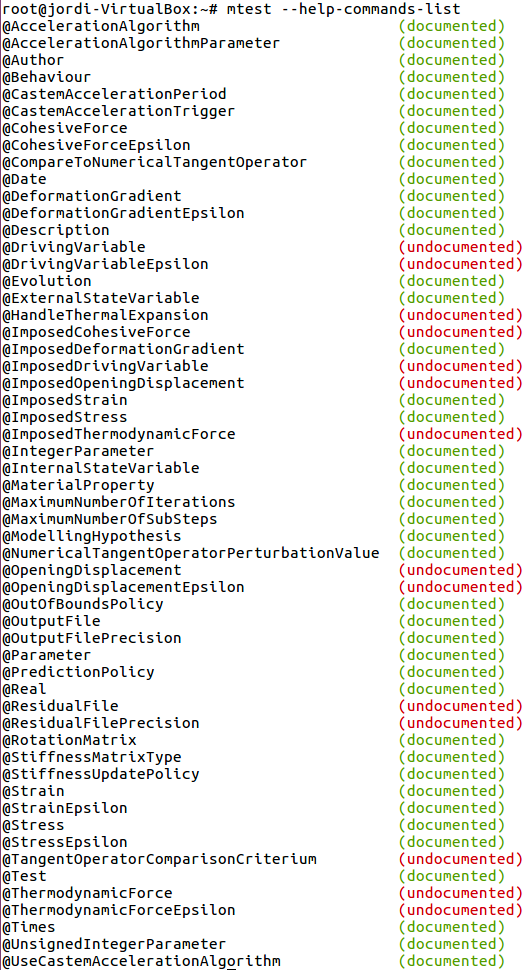
.mtestLos archivos .mtest toman la misma estructura que los
archivos .mfront. Se presentan como una lista de
instrucciones que empiezan por el símbolo @. Algunas de
estas instrucciones pueden tener opciones asociadas dadas entre los
símbolos < y >.
Comentarios: MTest también acepta los
dos tipos de comentarios de C++, es decir, los que empiezan por
/* y terminan por */ pudiendo estos ocupar
varias líneas, y los que empiezan por // extendiéndose
estos tan solo hasta el final de la línea actual.
Lectura de un número real: En varios lugares del archivo de entrada se requiere un número real. Si se proporciona una cadena, el contenido de esta cadena se interpreta como una fórmula matemática y es posible utilizar variables definidas anteriormente, siempre que sean constantes en el tiempo.
Descripción de una evolución temporal: La evolución en el tiempo de determinadas variables son datos esenciales para ser proporcionados por el usuario. Estos acontecimientos pueden ser reportados de dos maneras:
t, de forma explícita.A continuación, se detallarán algunas de las instrucciones más
significativas de MTest.
@Author: se utiliza para dar el nombre de la persona que
escribió el archivo .mtest.
@Author Jordi Alberich;@Behaviour: declara el comportamiento utilizado para la
prueba. Esta instrucción debe ir seguida de una opción que especifique
la interfaz utilizada por el comportamiento. Están disponibles las
interfaces castem, cyrano y aster.
Se esperan dos cadenas, la biblioteca en la que se implementa el comporamiento, y el nombre de la función.
@Behaviour<castem> 'libMFrontCastemBehaviours.so' 'umatnorton';@CastemAccelerationPeriod especifica el número de
iteraciones entre dos llamadas al algoritmo de aceleración.
@CastemAccelerationPeriod 3;@Date permite al usuario especificar cuándo se escribió
el archivo .mtest.
@Date 2016-11-28;@Description permite dar una descripción del test
implementado en el archivo.
@Description{
"Descripción del test a realizar"
}@Evolution especifica una función del tiempo.
Esta instrucción puede tener una opción, que es la forma en que se definirá la evolución. Se aceptan dos valores: evolution y function. Si no se especifica ninguna opción, se elige la opción de evolution.
A continuación se define, en forma de cadena, el nombre de la evolución.
Si se ha seleccionado la opción de evolution, el usuario puede especificar una evolución constante simplemente dando su valor. De lo contrario, las evoluciones complejas se pueden construir utilizando una matriz asociativa donde la clave es el tiempo y el valor de la evolución. Entre dos tiempos, los valores serán interpolados linealmente. Antes del primer tiempo declarado dado, se utiliza el valor correspondiente a esta primera vez. Después de la última vez dada, se utiliza el valor correspondiente a esta última vez.
Si se ha seleccionado la opción de function, se espera una cadena que
se interpretará como una función del tiempo. El tiempo está representado
por la variable t.
//Evolución constante
@Evolution 'Pressure' 1.e5;
//Evolución lineal
@Evolution 'Pressure' {0:0.,1.:1.e5};
//Función
@Real P0 2.e5
@Real P1 4.e5
@Evolution<function> 'Pressure' 'P0+(P1-P0)\*t\*\*2';@ExternalStateVariable permite al usuario especificar la
evolución de las variables de estado externas, incluida la temperatura
que generalmente se define por defecto en las interfaces de
comportamiento.
Esta instrucción puede tener una opción asociada, que es la forma en
que se definirá la evolución. Al igual que en la instrucción
@Evolution, se aceptan dos valores, evolution y
function.
//Evolución constante
@ExternalStateVariable 'Temperature' 293.15;
//Evolución lineal
@ExternalStateVariable 'Temperature' {0:293.15,1.:800};
//Función
@Real T0 293.15
@Real T1 400.15
@ExternalStateVariable<function>'Temperature''T0+(T1-T0)\*t\*\*2';@ImposedStrain permite al usuario imponer la evolución
de un componente de las tensiones.
Esta instrucción puede tener asociada una opción que corresponde a la forma en que se definirá la evolución, pudiendo ser evolution o function (evolution por defecto). A continuación, se especificará el nombre del componente de las tensiones.
Son válidos los siguientes nombres de componentes según la hipótesis de modelado:
AxisymmetricalGeneralisedPlaneStrain: ERR EZZ ETT.Axisymmetrical: ERR EZZ ETT ERZ.PlaneStress: EXX EYY EZZ EXY.PlaneStrain: EXX EYY EXY.GeneralisedPlaneStrain: EXX EYY EZZ EXY.Tridimensional: EXX EYY EZZ EXY EXZ EYZ.//Evolución constante
@ImposedStrain<evolution> 'EXX' 1e-3;
//Evolución lineal
@ImposedStrain<evolution> 'EXX' {0.:0.,1:1e-3};
//Función
@ImposedStrain<function> 'EXX' 'e0\*sin(t/900.)';@ImposedStress permite al usuario imponer la evolución
de un componente de estrés.
El funcionamiento de esta instrucción es igual al de la anterior
(@ImposedStrain), siendo válidos los siguientes nombres
según la hipótesis de modelado:
AxisymmetricalGeneralisedPlaneStrain: SRR SZZ STT.Axisymmetrical: SRR SZZ STT SRZ.PlaneStress: SXX SYY SXY.PlaneStrain: SXX SYY SZZ SXY.GeneralisedPlaneStrain: SXX SYY SZZ SXY.Tridimensional: SXX SYY SZZ SXY SXZ SYZ.//Evolución constante
@ImposedStress 'SXX' 50.e6;
//Evolución lineal
@ImposedStress<evolution> 'SXX' {0.:0.,1:50e6};
//Función
@ImposedStress<function> 'SXX' 's0\*sin(t/900.)';@InternalStateVariable define el valor inicial de una
variable de estado.
Si esta variable de estado interna es escalar, se espera un valor real. En cambio, si esta variable de estado interna es un tensor simétrico, se espera una matriz de valores reales del tamaño apropiado. Un tensor simétrico tiene 3 componentes en 1D, 4 componentes en 2D y 6 componentes en 3D. Los componentes fuera de las diagonales se declararán con un factor \(\sqrt{2}\).
@InternalStateVariable 'ElasticStrain' {'EELRR0' , 'EELZZ0' , 'EELZZ0',0.};@MaterialProperty define una propiedad de material. Sólo
pueden usarse las propiedades mecánicas definidas por el comportamiento
para la hipótesis de modelado considerada con la excepción de las
expansiones térmicas:
ThermalExpansion.ThermalExpansion1,
ThermalExpansion2 y ThermalExpansion3.A esta instrucción se le asocia como opción el tipo de propiedad material, pudiendo ser:
constant: se deberá indicar su valor.castem: se deberá indicar el nombre de la biblioteca y
el nombre de la función que implementa la propiedad material.function: se deberá definir la función.//constant
@MaterialProperty<constant> 'YoungModulus' 150.e9;
//castem
@MaterialProperty<castem> 'YoungModulus' 'libIncone1600MaterialProperties.so' 'Incone1600_YoungModulus';@Parameter especifica el valor de un parámetro real del
comportamiento.
@Parameter 'epsilon' 1.e-8;@IntegerParameter especifica el valor de un parámetro
entero del comportamiento.
@IntegerParameter 'iter' 12;@UnsignedIntegerParameter especifica el valor de un
parámetro entero positivo del comportamiento.
@UnsignedIntegerParameter 'iterMax' 12;@MaximumNumberOfIterations permite al usuario
especificar el número máximo de iteraciones del algoritmo global para
alcanzar el equilibrio.
Si el número de iteraciones alcanza el valor máximo autorizado, el
paso de tiempo se divide por dos. El número máximo de sub-pasos se puede
especificar usando la instrucción
@MaximumNumberOfSubSteps.
@MaximumNumberOfIterations 10;@MaximumNumberOfSubSteps permite al usuario especificar
el número máximo de sub-pasos permitidos.
Cuando el algoritmo global no alcanza el equilibrio, el paso de tiempo puede dividirse por dos. El número máximo de veces que el paso de tiempo se reduce se da por el número máximo de sub-pasos.
@MaximumNumberOsSubSteps 10;@ModellingHypotesis permite al usuario elegir la
hipótesis de modelado a utilizar. Se admiten los siguientes valores
dados como una cadena:
AxisymmetricalGeneralisedPlaneStrain (1D).Axisymmetrical (2D).PlaneStress (2D).PlaneStrain (2D).GeneralisedPlaneStrain (2D).Tridimensional (3D).La hipótesis de modelado cambia el nombre de los componentes de los
tensores simétricos y sus números como se ha visto en
@ImposedStrain y @ImposedStress.
@OutputFile especifica el nombre del archivo de salida.
De forma predeterminada, el nombre del archivo de salida es igual al
nombre de entrada con la extensión ‘.res’.
@OutputFile 'results.txt';@OutputFilePrecision especifica el número de dígitos
utilizados para imprimir los resultados en el archivo de salida.
@OutputFilePrecision 15;@PredictionPolicy le permite al usuario definir cómo se
obtendrá la estimación inicial de la solución, pudiendo ser:
NopredictionLinearPredictionElasticPredictionElasticPredictionFromMaterialPropertiesSecantPredictionTangentPrediction@PredictionPolicy 'ElasticPrediction';@Real permite al usuario definir una constante.
@Real 'SXX0' 20.6;@RotationMatrix permite al usuario especificar una
matriz de rotación, de manera que las direcciones principales del
material sean diferentes de las utilizadas para la resolución y las
condiciones de contorno.
@RotationMatrix {{0,1,0},
{1,0,0},
{0,0,1}};@StiffnessMatrixType permite al usuario especificar el
tipo de matriz de rigidez que debe ser dada por el comportamiento
mecánico y que será utilizado por el algoritmo de resolución. Son
válidos los siguientes valores:
ElasticSecantOperatorTangentOperatorConsistentTangentOperator@StiffnessMatrixType 'Elastic';@Strain permite al usuario especificar el valor inicial
de las tensiones.
Se debe especificar una matriz, donde el tamaño de este array debe ser igual al número de componentes de los tensores simétricos para la hipótesis de modelado considerada.
Los valores deben seguir las convenciones TFEL. En 3D, las tensiones están almacenadas en el siguiente orden:
\[\left( \text{varepsilon}_{\text{xx}},\varepsilon_{\text{yy}},\varepsilon_{\text{zz}},{\sqrt{2}\varepsilon}_{\text{xy}},{\sqrt{2}\varepsilon}_{\text{xz}},{\sqrt{2}\varepsilon}_{\text{yz}} \right)\]
@Strain { 0.000239466253465591,
-7.18398760396772e-05,
-7.18398760396772e-05,
0., 0., 0.};@Stress permite al usuario especificar el valor inicial
del estrés.
Se debe especificar una matriz, donde el tamaño de este array debe ser igual al número de componentes de los tensores simétricos para la hipótesis de modelado considerada.
@Stress {'YoungModulus\*EXX0',
'-PoissonRatio\*YoungModulus\*EXX0',
'-PoissonRatio\*YoungModulus\*EXX0',
0., 0., 0.};@StressEpsilon. El algoritmo global utiliza dos
criterios para comprobar si se ha encontrado un equilibrio
satisfactorio: uno sobre las tensiones y el otro sobre el estrés.
Este criterio sobre el estrés comprueba que el residuo del Algoritmo de Newton es bajo. Por defecto este valor es 1.e-3.
La instrucción @StressEpsilon permite al usuario
especificar el criterio de valor utilizado para el criterio de
estrés.
@StressEpsilon 1.e2;@Test permite al usuario añadir una prueba a los
resultados. Se admiten dos tipos de pruebas:
function: se permiten dos sintaxis. En la primera, se
esperan tres argumentos: el nombre de la variable probada, una función
del tiempo y un valor de criterio utilizado para la comparación. En la
segunda sintaxis, se esperan dos argumentos: un mapa que asocia el
nombre de una variable probada a una función de tiempo y un valor de
criterio utilizado para la comparación. Las funciones pueden depender
explícitamente del tiempo a través de la variable t.@Test<function> 'EXY' '0.' 1.e-12;
@Test<function>{ 'EXX': 'SXX/YoungModulus',
'EYY': '-PoissonRatio\*SXX/YoungModulus',
'EZZ': '-PoissonRatio\*SXX/YoungModulus',
'EXY': '0.','EXZ:'0.','EYZ':'0.'}1.e-12;file: los valores esperados se leen en columnas de un
archivo de texto. Se dará el nombre del archivo de texto y se permitirán
dos sintaxis. En la primera, se esperan tres argumentos: el nombre de la
variable probada, el número de columna y un criterio utilizado para la
comparación. En la segunda sintaxis, se esperan dos argumentos: un mapa
que asocia el nombre de la variable probada a un número de columna y un
criterio utilizado para la comparación. En cada caso, los valores dados
por la línea ‘n+1’ corresponden a los valores esperados después del
periodo ‘n’.@Test<file> 'reference.txt' 'EXY' 1 1.e-12;@Times permite al usuario especificar una lista de
tiempos utilizados para los cálculos.
Esto se especificará con una matriz que describe los intervalos de tiempo. De forma predeterminada, se utiliza un paso de tiempo para pasar de un momento dado al siguiente. El comando ‘in’ permite al usuario dividir un intervalo en un número dado de intervalos más pequeños.
@Times {0., 3600.}; /* 1 paso de tiempo de 3600. Segundos */
@Times {0., 3600. in 10}; /*10 pasos de tiempo de 360 segundos */Para empezar, se debería definir qué es la plataforma
SALOME, la cual es una plataforma genérica de
Pre-procesamiento y Post-procesamiento para simulaciones numéricas
desarrollada por EDF (Électricité de France). Es un programa de código
abierto (licencia LGPL) el cual se basa en una arquitectura abierta y
flexible hecha de herramientas propias e integrando otras herramientas
del mundo del software de código abierto, así como otras herramientas
comerciales con licencias de código cerrado.
Por otra parte, CODE-ASTER es una aplicación de elementos finitos, desarrollado también por EDF. Creado principalmente para el área de cálculos mecánicos, cubre un gran número de aplicaciones como pueden ser análisis térmicos y mecánicos tanto lineales como no lineales, fatiga, análisis de fracturas, etc.
Code-Aster ofrece una versión modificada de Salome a la cual le
incluye distintas herramientas para poder trabajar con este solver FEM,
llamada SALOME-MECA. Además del propio solver, Salome-Meca
incluye también herramientas para trabajar con Code-Aster como
Eficas con el que podemos escribir los casos FEM mediante
una interfaz gráfica la cual da acceso a todos los comandos posibles y
evalúa los pasos necesarios para cumplir con cada comando. Con
ASTK se puede manejar y configurar las simulaciones a
realizar.
Así, las principales características de Salome-Meca son:
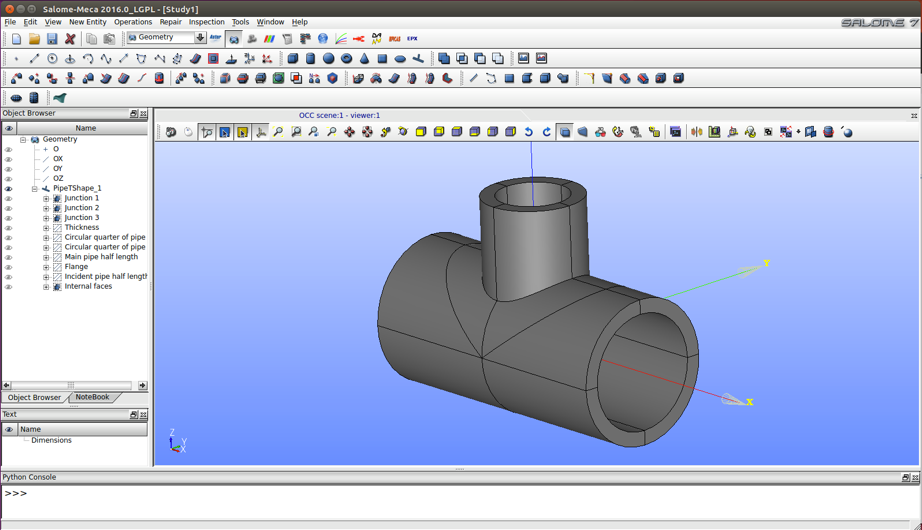
Módulo de geometría (Geometry): donde
se puede crear la geometría del problema a analizar, o incluso se puede
importar de otros programas.
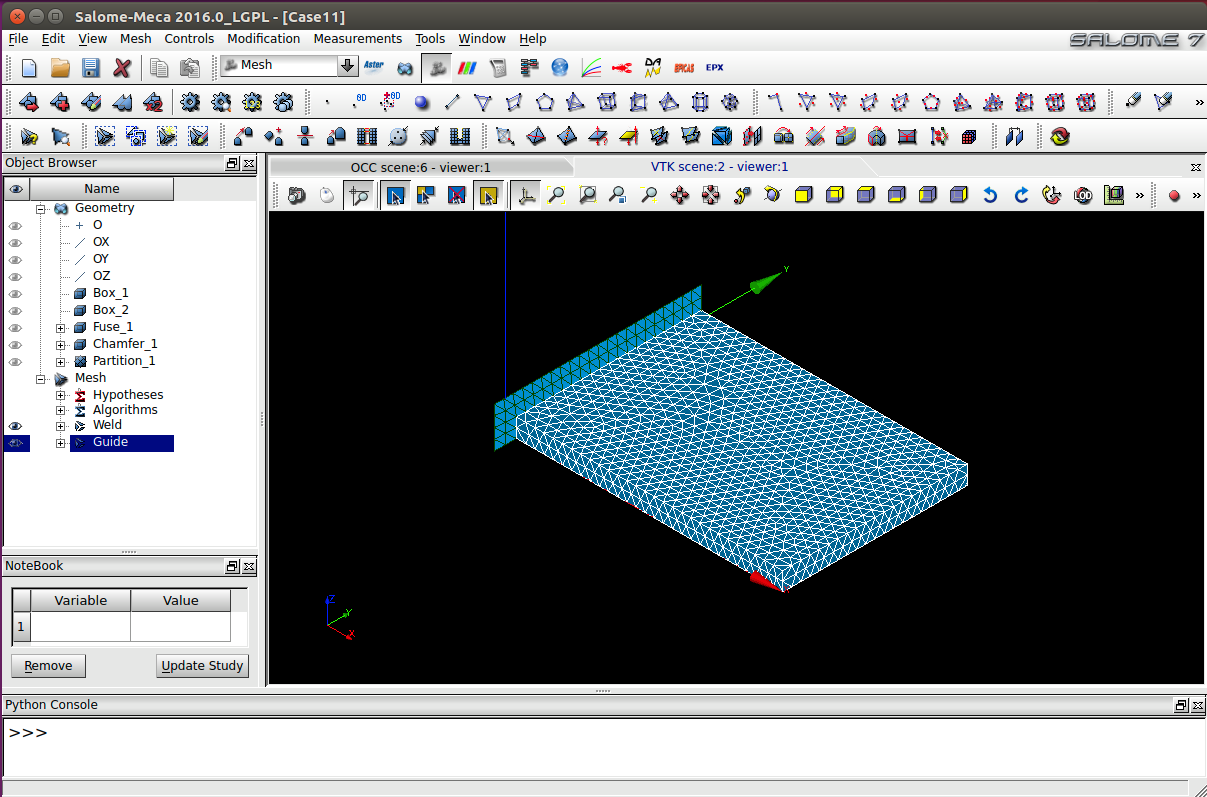
Módulo de mallado (Mesh): es usado para
generar mallas 1D, 2D o 3D para los análisis numéricos. Para ello cuenta
con varios algoritmos de mallado propios.
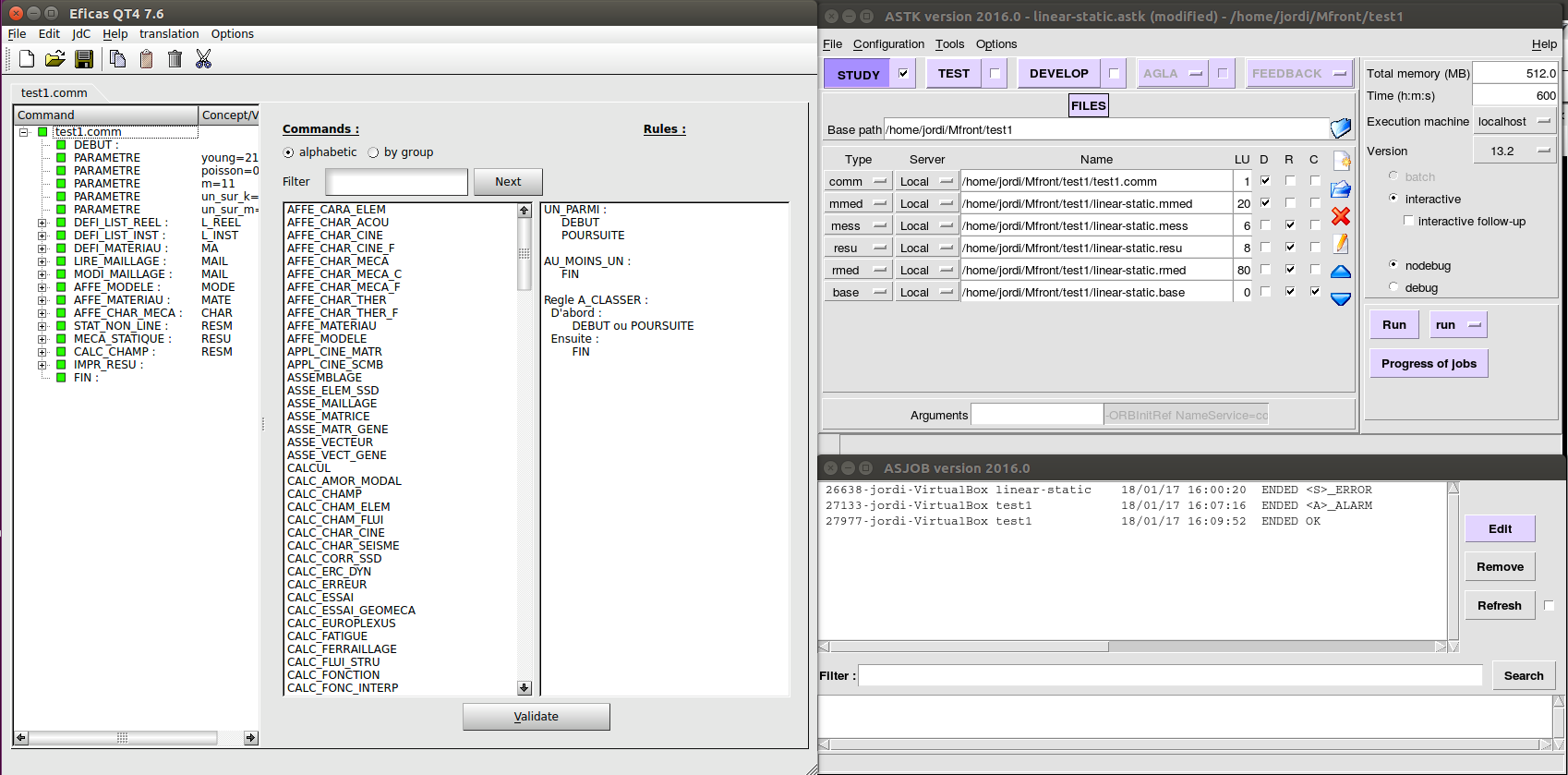
Módulo de Code-Aster (Aster): como se
ha descrito anteriormente, Aster és un módulo destinado al área de
cálculos mecánicos que incluye las herramientas Eficas y Astk.
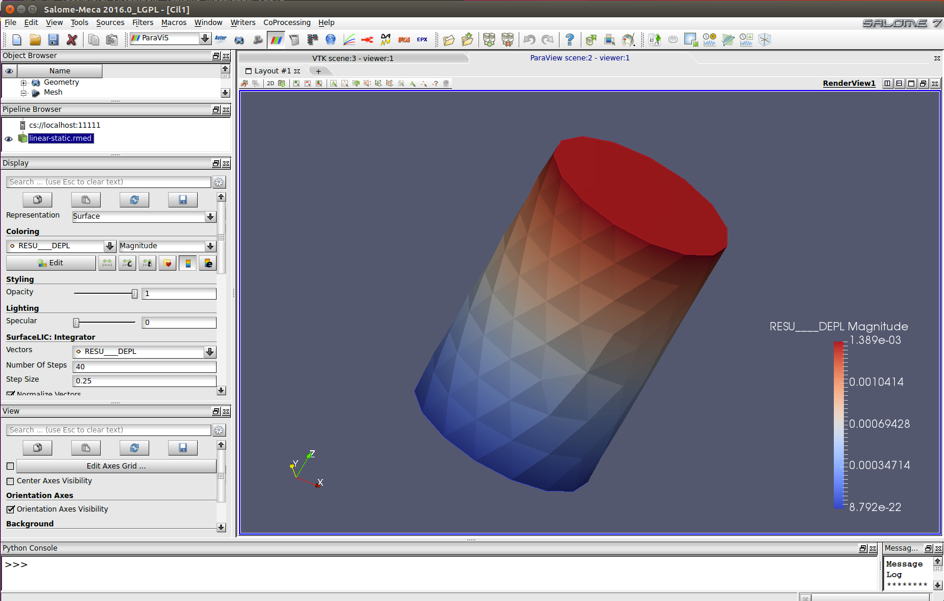
Módulo de post-procesamiento (ParaViS):
éste módulo se usa para analizar los resultados de la simulación
incluyendo el software para post-procesamiento ParaView, el cual tiene
un sin fin de herramientas utilizando técnicas cualitativas y
cuantitativas de utilidad para poder usar en el post-procesamiento de
nuestros análisis numéricos.
Al realizar un estudio con Salome-Meca, puede resultar interesante, o
de utilidad, añadir algún tipo de comportamiento del material, algo que
como se ha visto en los puntos anteriores se puede definir con
MFront.
Entonces, a lo largo de este punto se describirá, mediante un ejemplo, como se puede añadir dicho comportamiento empezando con la generación de éste y sus librerías, seguido de la creación del estudio en Salome-Meca y acabando con la inclusión de este comportamiento en el módulo Aster.
MFrontPara ver un ejemplo de cómo introducir una librería de comportamiento
material en un estudio en Salome-Meca, se procederá con la ley de
comportamiento viscoplástico de Lemaitre, cuyo modelo escrito de forma
implícita en MFront será el que se muestra en la
Ilustración 12 que puede ser escrito con un editor de texto genérico, y
luego se guardará el archivo con la extensión ’.mfront’:
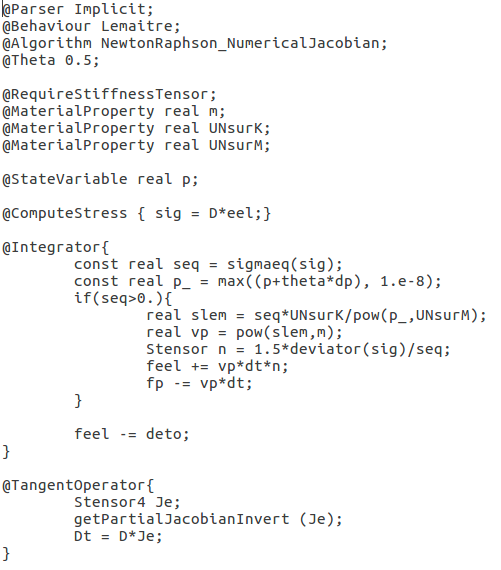
La compilación del archivo se ejecutará a través del Terminal, donde con el comando `–interface” se le indica el lenguaje destino con el que se quiere usar la librería.
$ mfront --obuild --interface=aster Lemaitre.mfrontUna vez compilado el archivo, si no hay ningún error en él,
MFront genera dos nuevos directorios en el directorio
actual para almacenar los archivos generados como se puede ver en la
Ilustración 13
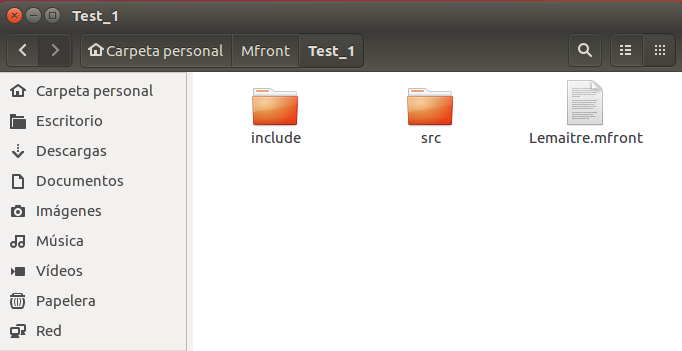
La librería generada necesaria para su uso en Salome-Meca, se
encuentra dentro del directorio src y se llama
libAsterBehaviour.so.
Antes de incluir la librería generada en el punto anterior, se debe generar el modelo que se quiere estudiar en Salome-Meca.
Para ello, se debe ejecutar desde el terminal Salome-Meca desde el directorio donde está instalado (generalmente en /root/salome_meca/appli_V2016/):
:/root/salome_meca/appli_V2016 $ ./salome
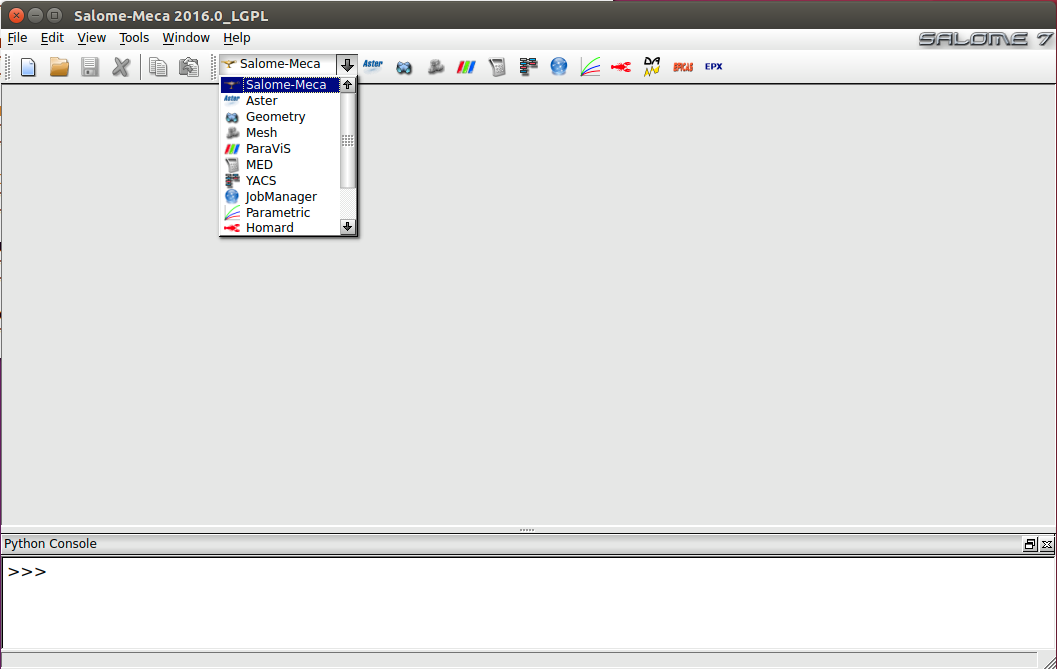
Una vez se haya cargado Salome-Meca, su pantalla inicial será como la que se muestra en la Ilustración 14, donde se puede ver que en la parte superior se encuentran las herramientas básicas de cualquier programa (‘nuevo documento’, ‘abrir documento’, ‘guardar’, etc.), y a la izquierda de estas herramientas, se encuentran los distintos módulos disponibles de Salome-Meca, seleccionables desde el menú desplegable, o directamente desde los botones a la derecha de este.
Estas herramientas son: Aster,JobManager,
Geometry,Parametric, Mesh,Homard,
ParaVis,ADAO, MED,Eficas, `YACS,
Y finalmente, al pie del programa, se puede encontrar una consola Python para poder trabajar en lenguaje Python.
Para empezar a crear un modelo de estudio útil para el ejemplo
actual, se deberá seleccionar el módulo Geometry donde
aparecerá un dialogo donde preguntará si se desea crear un nuevo
proyecto, o abrir uno ya existente.
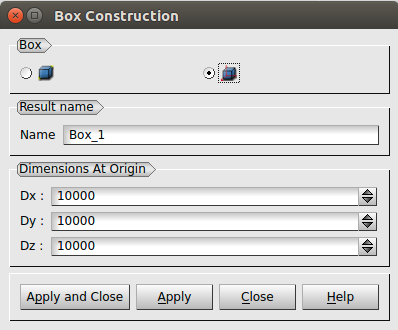
Una vez activado el módulo Geometry, en la barra de menús principal, se clicará sobre el menú New Entity Primitives Box, y emergerá una ventana de dialogo en la que se deberá seleccionar el segundo algoritmo del apartado Box y se dejará el resto tal y como aparece en la Ilustración 15 y para finalizar se clicará el botón de Apply and Close.
Esto generará un cubo de las dimensiones especificadas, teniendo el aspecto de la Ilustración 16.
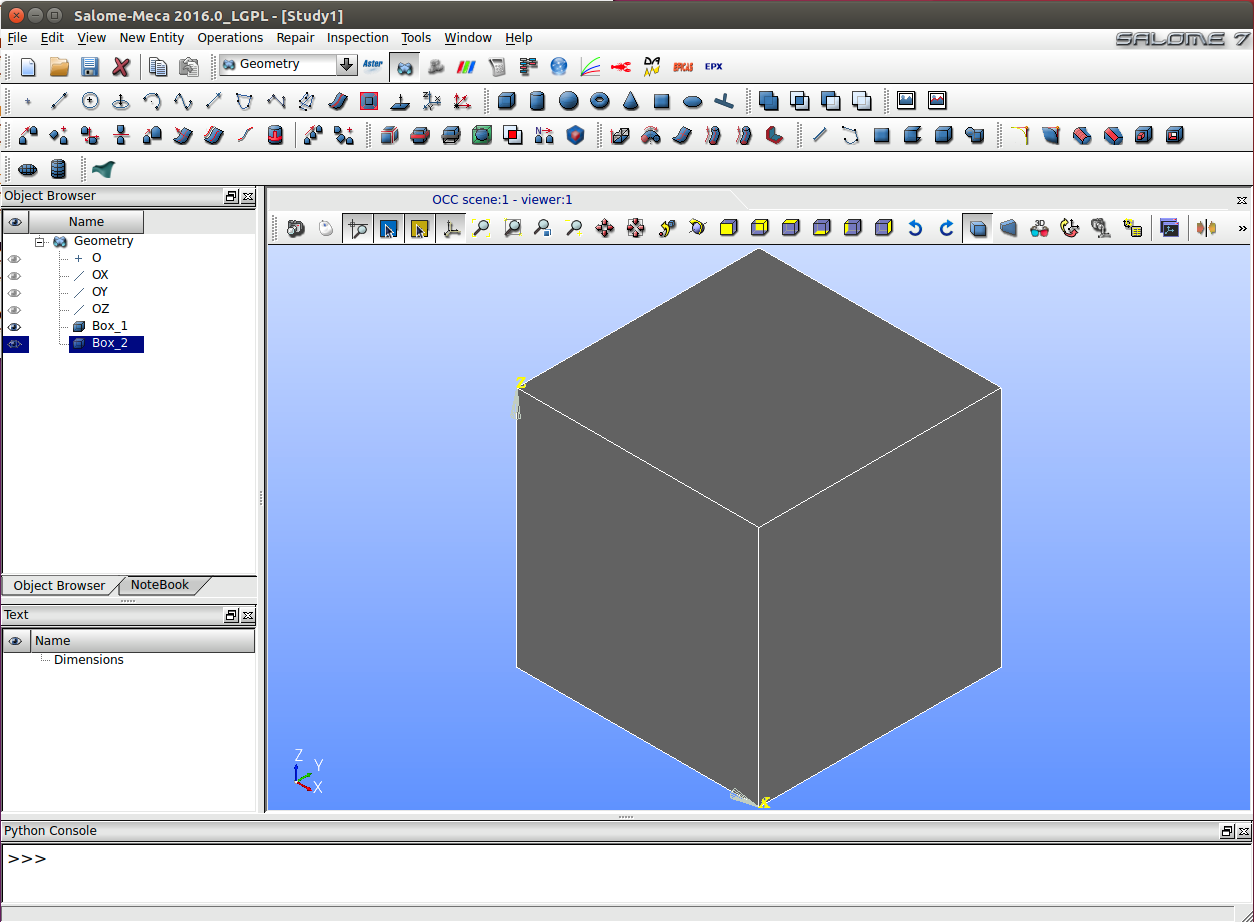
El siguiente paso consiste en crear grupos que serán útiles para el análisis de elementos finitos. Para ello se debe seleccionar la opción New Entity Group Create Group.
Se deberá seleccionar la tercera opción en Shape Type para poder
seleccionar una cara entera del cubo. En el campo Name se
le pondrá el nombre que se le quiera dar al grupo, en este caso
Fix. En el campo Main Shape, si la geometría creada ya
estaba seleccionada, aparecerá en el campo automáticamente, sino, tan
solo es necesario clicar sobre el botón de la flecha y seleccionar la
geometría sobre la que se quieren crear los grupos. A continuación, se
rotará el cubo hasta que sea visible la cara inferior de este para poder
seleccionarla, y se clicará sobre el botón Add para que se pueda añadir
la selección como aparece en la Ilustración 17, se clicará sobre el
botón inferior Apply, y se repetirá este proceso cambiando el campo Name
a Press, y seleccionando la cara superior del cubo.
Finalmente, ya se puede clicar sobre Apply and Close.
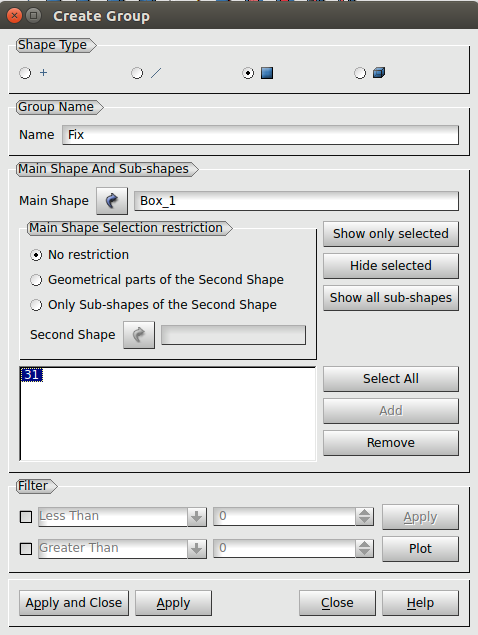
Esto habrá creado los dos grupos sobre la geometría generada y el navegador de objetos deberá tener el siguiente aspecto de la Ilustración 18.
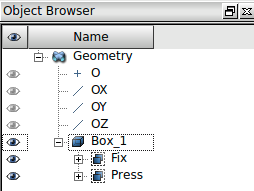
Y con ello quedará concluida la creación del objeto de estudio sobre el módulo de geometría.
El siguiente paso ahora, es crear un mallado del objeto creado en el
punto anterior para que se pueda hacer el estudio correspondiente, para
ello se debe seleccionar el módulo Mesh de Salome-Meca.
Una vez cargado el módulo, se creará el mallado desde el menú
principal Mesh Create Mesh lo cual mostrará la ventana de la Ilustración
19 donde se seleccionará la geometría creada en el punto anterior
Box_1, y se seleccionará en el campo Algorithm el algoritmo
Netgen 1D-2D-3D, y en el campo Hypothesis se deberá clicar sobre el
botón con forma de tuerca a la derecha de este campo, y se seleccionará
la opción NETGEN 3D Parameters con lo que emergerá otra ventana con una
serie de parámetros que se dejarán en su valor predeterminado.
Finalmente, se podrá clicar sobre el botón de Apply and Close.
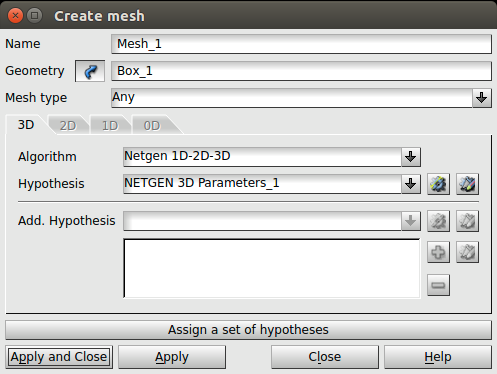
Esto añadirá los campos Hypotheses,
`Algorithms y Mesh_1 al navegador de
objetos.
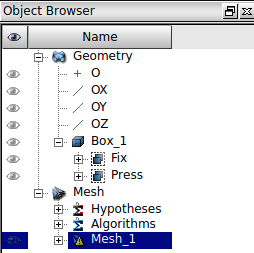
Ahora, haciendo clic derecho sobre el campo Mesh_1 que
aparece seleccionado en la Ilustración 20, se deberá clicar sobre la
opción Compute con el dibujo de una tuerca, que también se puede clicar
sobre el botón con este mismo dibujo que aparece debajo del menú
principal desplegable de los módulos de seleccionables.
Con esto, aparecerá una ventana como la de la Ilustración 21 con los resultados de la computación del mallado.
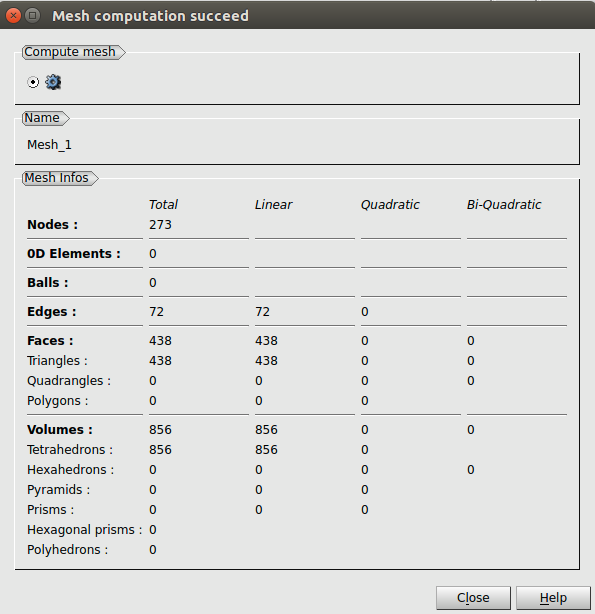
Quedando el objeto creado en el módulo de geometría mallado como aparece en la Ilustración 22.
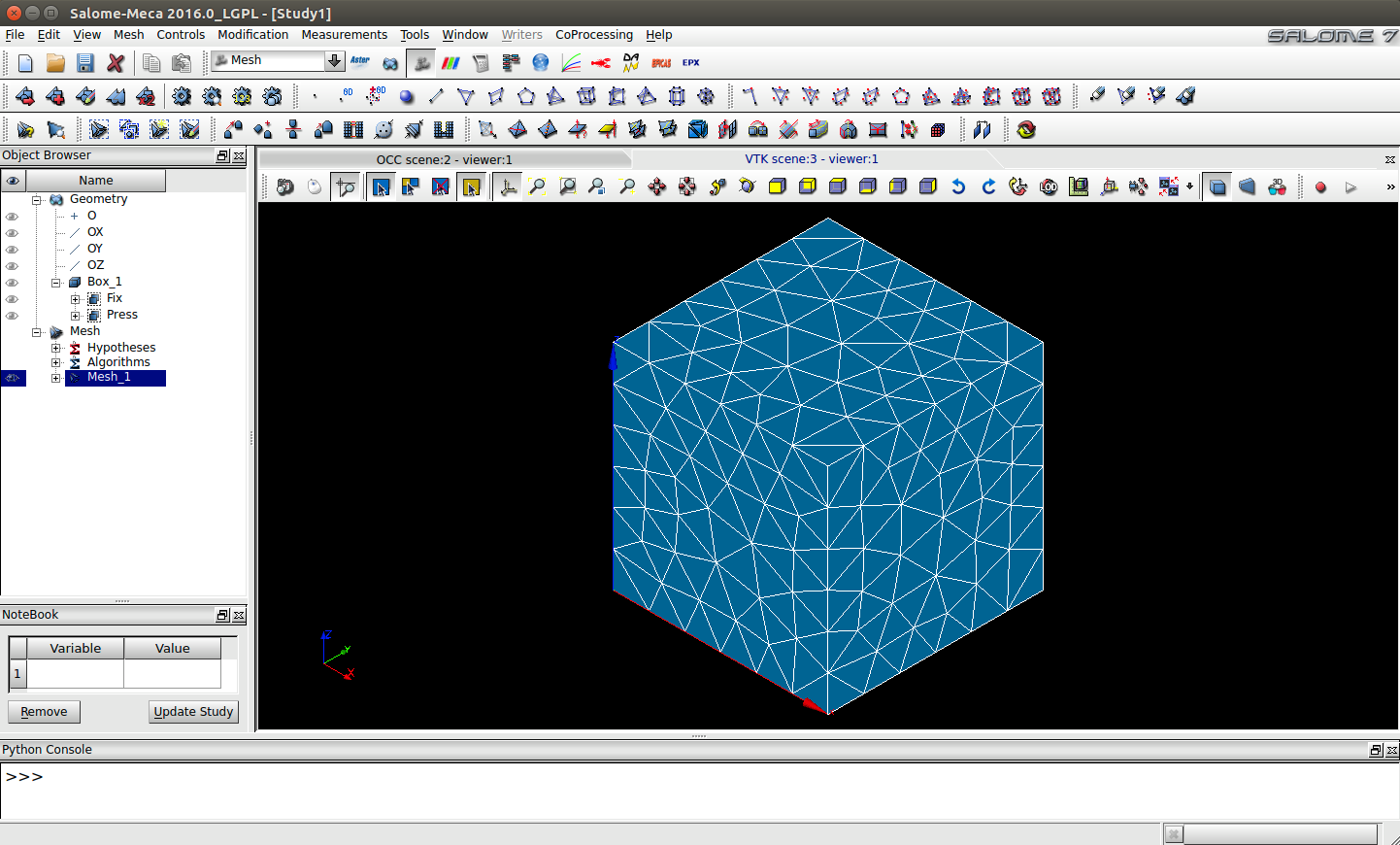
Habiendo creado el modelo geométrico y habiéndole dado grupos geométricos, y luego, habiendo creado un mallado 3D del modelo geométrico que será usado para el análisis de elementos finitos, ahora le toca el turno del módulo Aster de Salome-Meca.
Para ello, se debe seleccionar dicho módulo clicando sobre
Aster en el menú desplegable.
Asegurándose de que Mesh_1 sigue seleccionado, se deberá
acceder desde la barra de menús principal a la opción Aster Wizards
Linear elastic, esto abrirá el cuadro de dialogo de la Ilustración 23
done pide la definición del modelo.
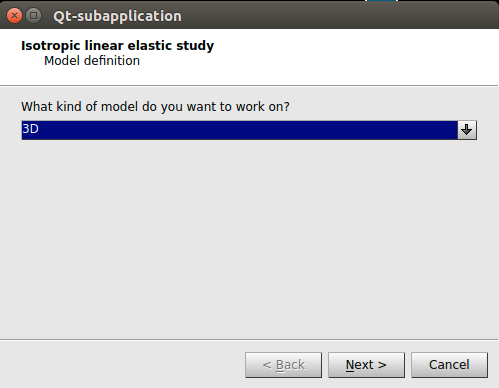
En el siguiente paso (Ilustración 24), pide seleccionar el mallado sobre el que se desea hacer el estudio.
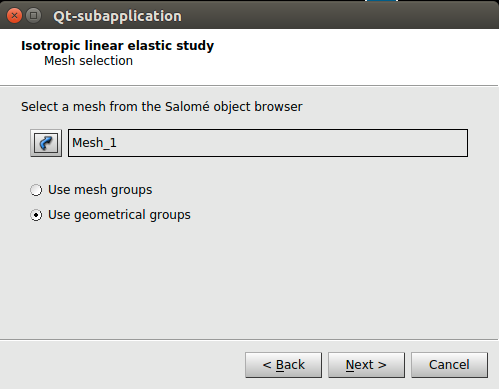
En el siguiente cuadro de dialogo (Ilustración 25), se deben indicar el valor de las propiedades del material.
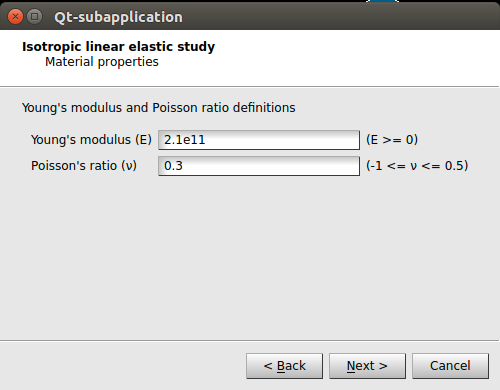
En los dos siguientes pasos (Ilustración 26), se pueden añadir condiciones de contorno al estudio.
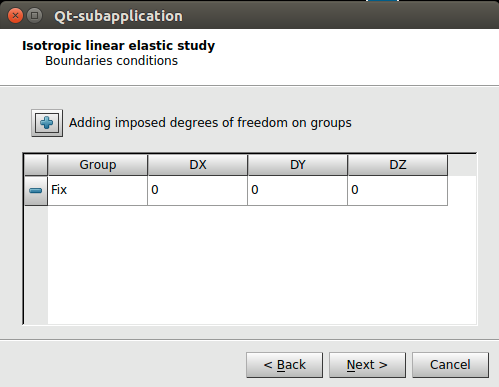
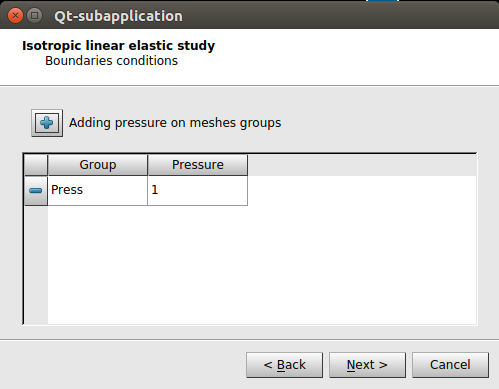
Y finalmente, en el último paso, se le debe indicar el nombre del
archivo de comandos .comm
Habiendo creado el estudio, aparecerán los nuevos campos (Ilustración 28) en el navegador de objetos.
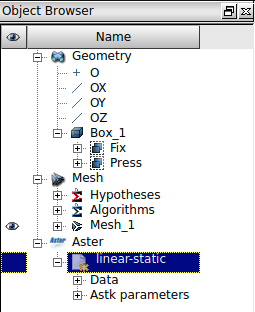
Y finalmente, se puede ejecutar el estudio haciendo clic derecho
sobre el estudio seleccionado en la ilustración anterior
(linear-static), y haciendo clic sobre la opción
Run. Esto entregará (después de pasar unos instantes de
computación) un mensaje de información, el cual indicará si todo ha
salido bien, o de lo contrario mostrará un mensaje de error. Además,
este mensaje indica que, si todo ha salido bien, se podrán ver los
resultados de la simulación en el módulo ParaViS.
Si la ejecución del estudio anterior ha concluido sin errores, se
pueden observar sus resultados en el módulo ParaViS, y para
ello se deberá activar dicho módulo desde el menú desplegable.
Si al activar el módulo ParaViS, en el lado izquierdo del programa
sigue viéndose tan solo el navegador de objetos, será necesario añadir
dos vistas adicionales desde el menú principal View Windows
Pipeline Browser y Display.
Sobre la nueva ventana que se añadirá al lado izquierdo del programa
llamada Pipeline Browser, se podrá hacer clic derecho y
luego clic sobre la opción Open para añadir el archivo de resultados
linear-static.rmed generado por el módulo Aster como
aparece en la Ilustración 29.
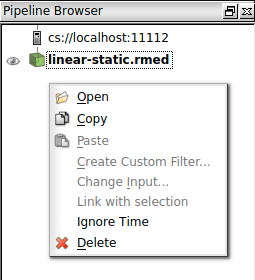
Una vez añadido el archivo de resultados, haciendo clic sobre el
icono situado a su izquierda con forma de ojo, se podrán ver los
resultados seleccionándolos desde el campo Coloring de la
ventana Display como se muestra en la Ilustración 30.
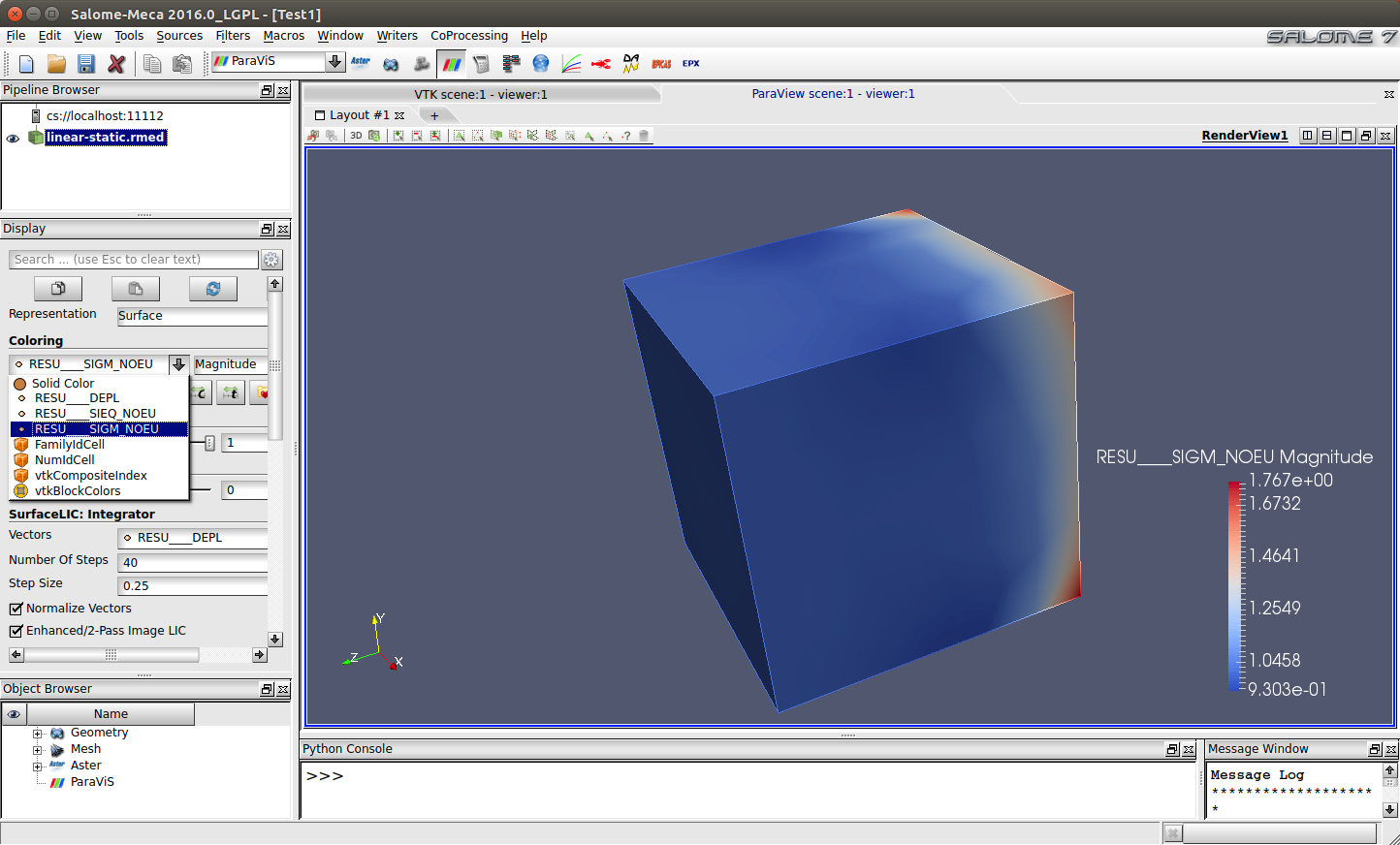
Para poder incluir la librería generada con MFront, se
debe modificar el archivo de comandos .comm creado en el
apartado ’
Cálculo mecánico con el módulo Aster’.
Para ello, hay dos opciones disponibles. La primera es modificar directamente el archivo con un editor de texto. Y la segunda y más recomendable, consiste en modificarlo mediante el programa EFICAS Aster el cual brinda la posibilidad de editar el archivo de comandos sin dar opción a errores de edición.
El primer paso para la inclusión de librerías MFront, es
asegurarse que la versión con la que se está trabajando de Aster sea
compatible con MFront, es decir, si la versión instalada de
Aster en Salome-Meca es superior a la 13.2 no habrá ningún problema,
pero en cambio, en la versión de Salome-Meca instalada para este
trabajo, la versión de Aster 13.2 estaba en fase de test, y por defecto
trabajaba con una versión anterior no compatible con
MFront.
Para poder trabajar con la versión 13.2, con el módulo
Aster activado, se deberá hacer clic derecho sobre el
estudio linear-static en el navegador de objetos y hacer clic
sobre la opción Edit, con lo que aparecerá la ventana de la Ilustración
31 donde se deberá seleccionar la versión 13.2 en el campo Aster
Version.
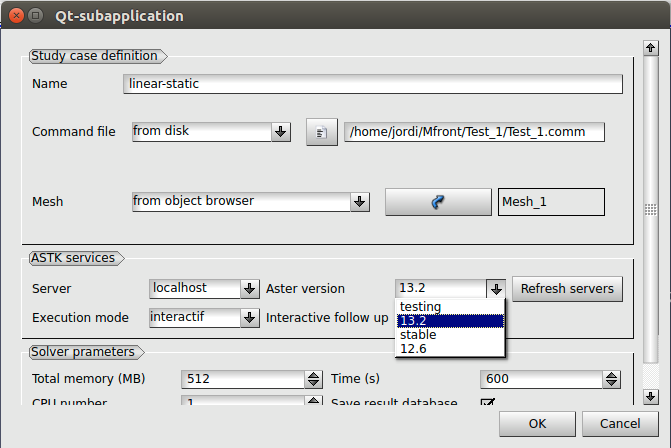
Ahora, clicando sobre el estudio linear-static del
navegador, aparecerán dos campos relativos a este. Donde desplegando el
campo Data aparecerá el archivo de comandos referente al
estudio configurado en el punto ’
Cálculo mecánico con el módulo Aster’. Haciendo clic derecho sobre este archivo se deberá hacer clic sobre la opción Run Eficas que, mostrará el siguiente mensaje (Ilustración 32), donde se deberá seleccionar la versión 13.2 de Aster.
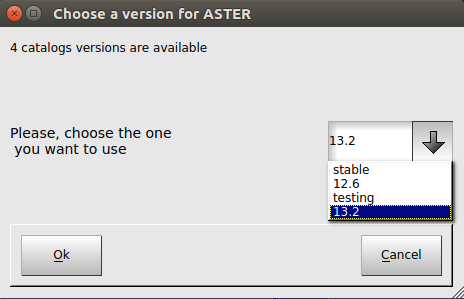
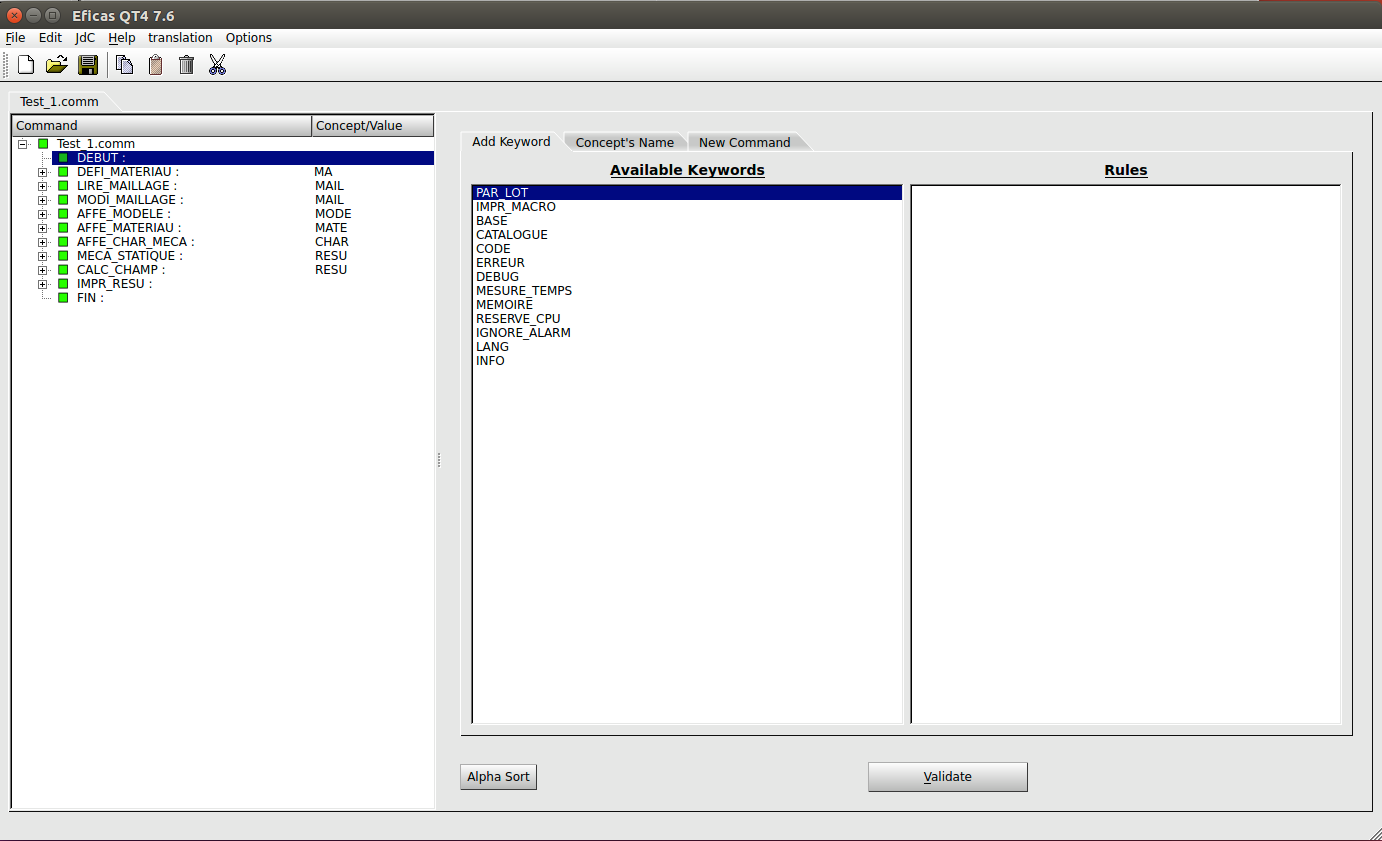
Una vez ya se ha seleccionado la opción, se ejecutará el programa
Eficas y tendrá el aspecto de la Ilustración 33, donde se
puede ver en el apartado izquierdo, los comandos incluidos en el archivo
actual, cada uno de ellos desplegable para mostrar sus parámetros
adicionales, en el apartado central se muestran las instrucciones o
parámetros disponibles, y finalmente en el derecho las reglas de uso de
la instrucción o parámetro seleccionado.
En la parte superior del bloque derecho aparecen tres pestañas. La primera (Add Keyword) es la que indica las instrucciones o parámetros disponibles según el comando seleccionado en la columna izquierda. La función de la segunda pestaña (Concept’s Name) es la de asignar un nombre al comando seleccionado. Y finalmente, la función de la última pestaña (New Command) es para añadir nuevos comandos.
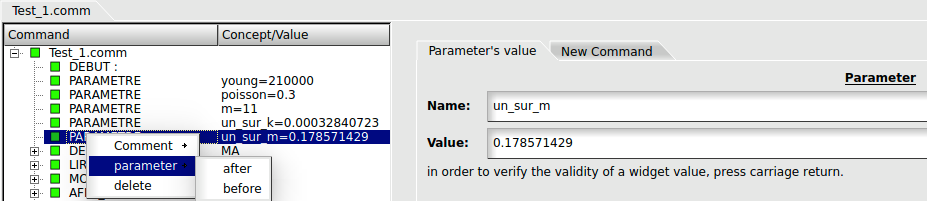
Además, haciendo clic derecho sobre la columna izquierda (donde
aparecen los comandos) se pueden añadir parámetros o comentarios. Así
que se puede empezar añadiendo los parámetros necesarios en el
comportamiento preparado con MFront que se quiera añadir al
estudio como se puede ver en la Ilustración 34.
El siguiente comando DEFI_MATERIAU que consiste en la definición de los parámetros describiendo el comportamiento de un material, ahora tiene definidos el parámetro E (coeficiente de Young) y NU (Poisson) que ya se habían definido al crear el estudio lineal elástico con Aster.
En este comando se deberán añadir los parámetros asociados al
comportamiento añadido con MFront, para ello se deberá
añadir la instrucción llamada MFRONT de la columna central cuando está
seleccionado el comando DEFI_MATERIAU. Añadida la
instrucción, aparecerá en la columna central un solo parámetro
disponible (LISTE_COEF) el cual se deberá añadir
también.
A continuación, se pueden añadir los valores de forma manual, añadiendo los valores a la lista (si no se hubieran definido previamente los parámetros Young, poisson, m, etc…), o se podrán añadir los valores directamente de los parámetros haciendo clic sobre el botón Parameters. Esto mostrará una lista de los parámetros definidos anteriormente y se podrán seleccionar los que interese y se deberá hacer clic sobre Validate una vez ya estén seleccionados.
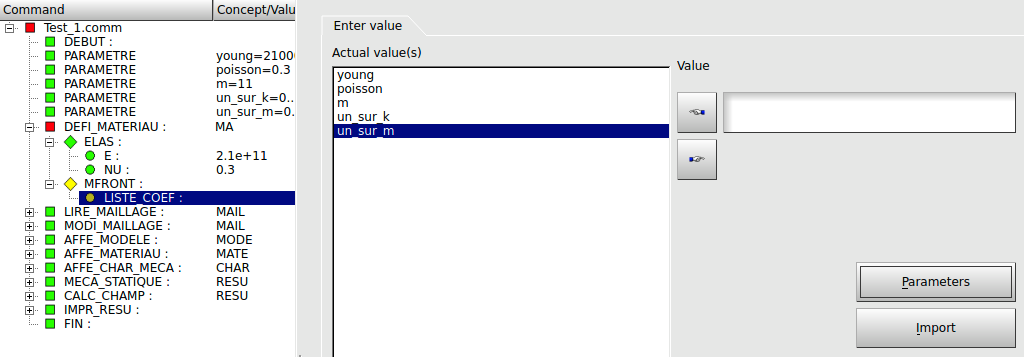
Mientras se está editando un comando, las figuras (cuadrados, rombos
y círculos) situados a la izquierda de cada parámetro o instrucción
aparecen en amarillo y en rojo para indicar que aún no está completa o
es errónea la edición del comando como se puede observar en la
Ilustración 35. Cuando la edición esté completa y sea correcta, estos
elementos aparecerán de color verde. Hay que recordar, que al final de
la edición de un nuevo comando, Eficas requiere la asignación de un
nombre del comando, en el caso de DEFI_MATERIAU viene
predefinido como MA.
Ahora, el siguiente punto consiste en añadir al fichero de comandos
la librería creada con MFront.
Para ello, se añadirá un comando de computación no lineal que pueden
ser STAT_NON_LINE, DYNA_NON_LINE o
SIMU_POINT_MAT. Seleccionando uno de estos comandos, se le
deberá añadir la instrucción COMPORTEMENT en la que se deberá indicar
que se trata de un comportamiento definido por MFRONT en el campo
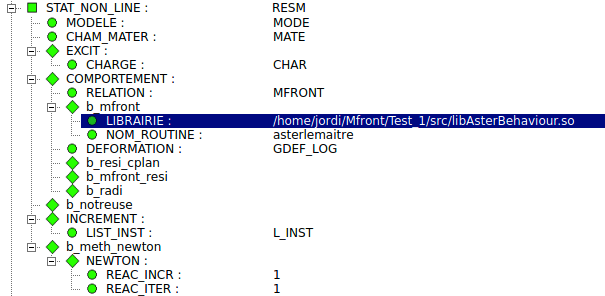
RELATION. Esto añadirá dos campos adicionales.
En el primero, LIBRARIE se le deberá indicar la ruta
completa de la librería que se desea añadir al estudio como se muestra
en la Ilustración 36.
Y en el segundo campo, NOM_ROUTINE, permite especificar
el modelo de comportamiento elegido, lo cual es útil si se han compilado
varias leyes juntas. Este nombre se construye con la concatenación de
aster con el nombre definido en la instrucción
@Behaviour del archivo MFront.
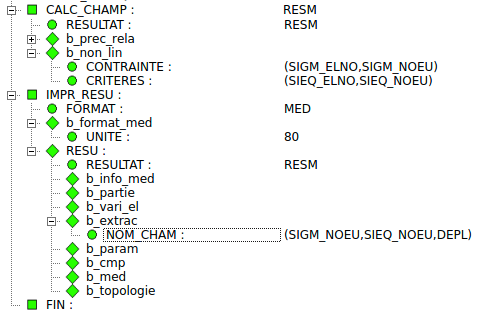
El último paso será añadir los cálculos que se deseen realizar en el
comando CALC_CHAMP indicándole en el campo RESULTAT que se
harán sobre el comportamiento añadido anterior (RESM) e
indicándole dichos análisis en el campo b_non_lin. Y
finalmente se deberán añadir estos análisis a la impresión de resultados
en el comando IMPR_RESU incluyéndolos en el campo b_extrac
como se muestra en la Ilustración 37.
Con esto (guardando el archivo editado .comm), se puede
dar por concluida la edición básica del archivo de comandos para la
inclusión de la librería del comportamiento editado con
MFront, quedando para el usuario la edición del resto de
comandos o parámetros del archivo según los intereses de este. (El
archivo .comm resultante de este ejemplo está incluido en el “Anexo 4:
Archivo de comandos Test_1.”)
Una vez editado el archivo de comandos, tan solo queda volver al módulo Aster y ejecutar el análisis.
Si el resultado de la ejecución es satisfactorio (Ilustración 38) tan solo queda ver los resultados en el módulo ParaVis (Ilustración 39)
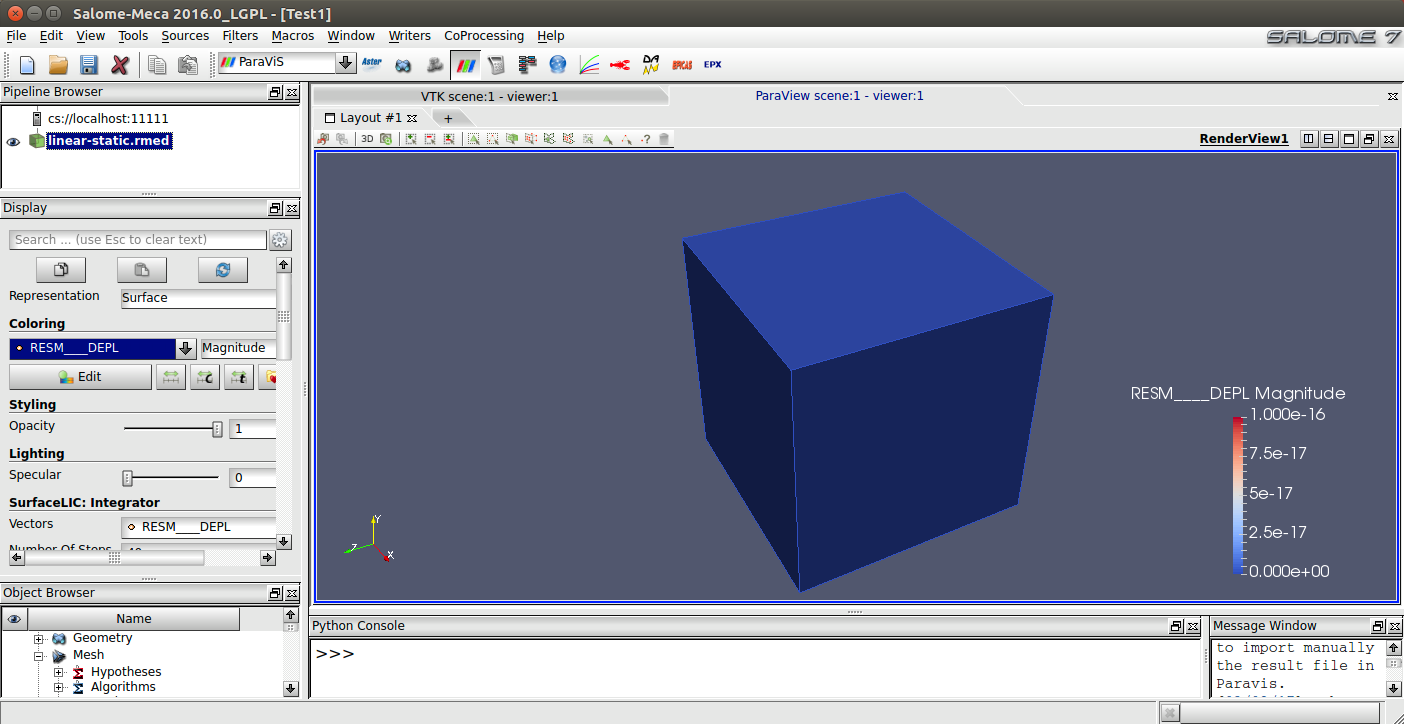
Si la ejecución del análisis reporta un mensaje de error (Ilustración
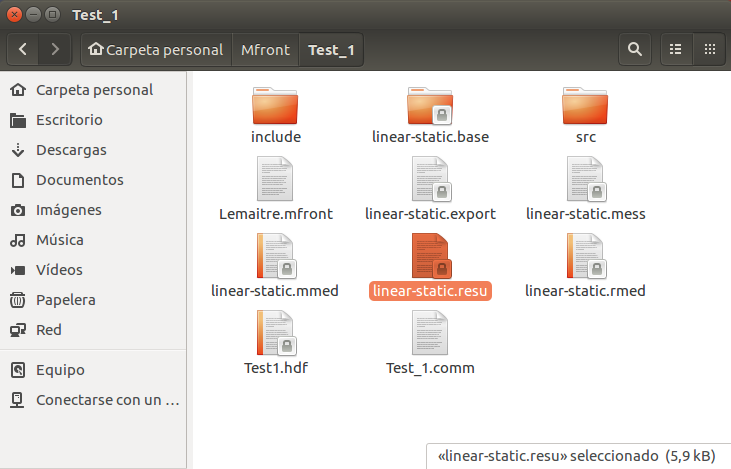
41), se puede consultar el error cometido en el archivo guardado en el
directorio (donde se han guardado el resto de los archivos del estudio)
con la extensión .resu (Ilustración 41)
El primero a tener en cuenta, es que, para utilizar los programas necesarios de este documento, se necesitará trabajar en un entorno Linux, por lo que, en el caso personal, se ha instalado un sistema Ubuntu desde una máquina virtual en un equipo Mac.
En este punto, y los siguientes, para evitar problemas de accesos a
determinados archivos o carpetas, se trabajará como root
desde el Terminal del sistema:
$ sudo –iPara el correcto funcionamiento de los programas que se mencionan en este documento, es necesaria la instalación de los siguientes paquetes antes de instalar los programas en cuestión:
gccneditcmakegeanypythongvimpython-devdddpython-numpyxmgracepython-qt4gracetkgnuplotbisonflexliblapack-devlibblas-devzlib1g-devCada uno de estos paquetes se instalará usando el siguiente comando
desde el terminal (trabajando como root):
$ apt install [nombre_paquete]Para la instalación del paquete de TFEL/MFRONT hay que tener en cuenta que TFEL ya forma parte de las versiones superiores a la 12.03 de Code-Aster y a las superiores a la 2015.1 de Salome-Meca, por lo que si ya se dispone de alguno de estos productos no será necesaria su instalación.
Se podrá descargar la última versión lanzada del producto desde la
página dedicada a la descarga de archivos de TFEL (https://github.com/thelfer/tfel/releases),
donde a fecha de realización de este trabajo, la última versión
disponible era la tfel-2.0.4.
Una vez ya se haya descargado el archivo
tfel-2.0.4.tar.bz2, se accederá al directorio de
descargas:
$ cd /home/*\[nombre_usuario\]*/DescargasY se descomprimirá el archivo descargado:
$ tar xvf tfel-2.0.4.tar.bz2Antes de proceder a la instalación del paquete descargado, hay que
asegurarse que la versión de cmake sea superior a la
2.8:
$ cmake --versionSi se cumple, ya se puede proceder a la instalación:
$ cmake \[opciones\]
$ make
$ make installDonde las opciones serán según las preferencias del usuario, por ejemplo, una instalación recomendada sería:
$ cmake –DCMAKE_BUILD_TYPE=Release –Dlocal-castem-header=ON
–Denable-fortran=ON –Denable-aster=ON –DCMAKE_INSTALL_PREFIX=
/root/tfelFinalmente, para asegurarse que la instalación se ha realizado correctamente, tan solo queda probarlo:

Para la instalación de Salome-Meca se podrá efectuar la descarga del
archivo desde la página oficial de Code-Aster (www.code-aster.org) donde en el
menú principal se deberá acceder a la sección de descargas
(Download o Téléchargement).
La sección de descargar dispone de un menú a la izquierda desde donde
se podrá acceder a la sección Salome-Meca y donde ya se podrá
descargar las distintas versiones lanzadas de Salome-Meca. La última al
día de la elaboración de este documento,
Salome-Meca 2016.
Entonces, una vez ya descargado el paquete deseado, se accede a la carpeta de descargas y se deberá descomprimir el binario descargado:
$ tar xvf SALOME-MECA-2016-LGPL-1.tgzY cuando se haya descomprimido, se puede ejecutar el instalador:
$ ./SMECA_V2016_LGPL.runCuando se haya instalado se podrá acceder donde se haya instalado (por defecto /root/salome_meca), y desde ese directorio, para ejecutar-lo:
$ cd appli_V2016
$ ./salomeEn este anexo se incluye el archivo resultante del apartado
“Modificación del archivo .comm para incluir la librería” donde se
modifica un archivo .comm ya generado con la ayuda del programa
EFICAS Aster para poder incluir en él una librería ya
generada con MFront.
En él se puede ver que los comandos importantes donde hay que fijarse para la inclusión de una librería en el estudio son:
DEFI_MATERIAU: donde se le deberá indicar que trabajará
con unos materiales definidos por MFRONT.
STAT_NON_LINE (o cualquier otro comando de computación):
donde se le deberá indicar la ruta completa de donde se encuentra la
librería en cuestión.
DEBUT();
young = 210000;
poisson = 0.3;
m = 11;
un_sur_k = 0.00032840723;
un_sur_m = 0.178571429;
L_REEL=DEFI_LIST_REEL(DEBUT=0.0,
INTERVALLE=(_F(JUSQU_A=0.02,
PAS=0.002,),
_F(JUSQU_A=0.06,
PAS=0.004,),
_F(JUSQU_A=0.24,
PAS=0.01,),),);
L_INST=DEFI_LIST_INST(DEFI_LIST=_F(METHODE='MANUEL',
LIST_INST=L_REEL,),);
MA=**DEFI_MATERIAU**(ELAS=_F(E=2.1e+11,
NU=0.3,),
**MFRONT=_F(LISTE_COEF=(young,poisson,m,un_sur_k,un_sur_m,),)**,);
MAIL=LIRE_MAILLAGE(FORMAT='MED',);
MAIL=MODI_MAILLAGE(reuse =MAIL,
MAILLAGE=MAIL,
ORIE_PEAU_3D=_F(GROUP_MA='Press',),);
MODE=AFFE_MODELE(MAILLAGE=MAIL,
AFFE=_F(TOUT='OUI',
PHENOMENE='MECANIQUE',
MODELISATION='3D',),);
MATE=AFFE_MATERIAU(MAILLAGE=MAIL,
AFFE=_F(TOUT='OUI',
MATER=MA,),);
CHAR=AFFE_CHAR_MECA(MODELE=MODE,
DDL_IMPO=_F(GROUP_MA='Fix',
DX=0.0,
DY=0.0,
DZ=0.0,),
PRES_REP=_F(GROUP_MA='Press',
PRES=1.0,),);
RESM=**STAT_NON_LINE**(MODELE=MODE,
CHAM_MATER=MATE,
EXCIT=_F(CHARGE=CHAR,),
**COMPORTEMENT=_F(RELATION='MFRONT',
LIBRAIRIE='/home/jordi/Mfront/Test_1/src/libAsterBehaviour.so',**
**NOM_ROUTINE='asterlemaitre',),**
INCREMENT=_F(LIST_INST=L_INST,),
NEWTON=_F(REAC_INCR=1,
REAC_ITER=1,),);
RESU=MECA_STATIQUE(MODELE=MODE,
CHAM_MATER=MATE,
EXCIT=_F(CHARGE=CHAR,),);
RESM=CALC_CHAMP(reuse =RESM,
RESULTAT=RESM,
PRECISION=1e-06,
CONTRAINTE=('SIGM_ELNO','SIGM_NOEU',),
CRITERES=('SIEQ_ELNO','SIEQ_NOEU',),);
IMPR_RESU(FORMAT='MED',
UNITE=80,
RESU=_F(RESULTAT=RESM,
NOM_CHAM=('SIGM_NOEU','SIEQ_NOEU','DEPL','SIGM_ELNO','SIEQ_ELNO',),),);
FIN();