This article shows how to implement the Méric-Cailletaud single crystal viscoplastic behaviour [1] in MFront. Such an example illustrates:

Advices

This kind of behaviour is rather complex and requires lot of care to get it work properly in any solver. We highly recommend that you follow these steps when implementing such behaviour:

  1. Validate the definition of your material orientation on a simple orthotropic behaviour.
  2. Validate the definition of the slips systems and the interaction matrix using mfront-query as advocated on this page.
  3. Start validating the behaviour without isotropic hardening nor kinematic hardening, then add the isotropic hardening and finally the kinematic hardenings.
  4. Start by using a numerical jacobian, then compute each terms of the jacobian analytically (see the @NumericallyComputedJacobianBlocks keyword to compute one block at a time).
  5. Watch out that most implementation of the Méric-Calletaud uses a very high value for the stress exponent (typically \(70\) to \(100\)) which may lead to many divergences of a standard Newton-Raphson algorithm. This issue is discussed at the end of this document.

The implementations described in this document are available here:

Description of the behaviour

The theoretical frame which allow the monocrystalline model was introduced in the 70. Monocrystalline behaviour describes the slip of the crystallographic structure through the slip systems of the considerated crystal. The crystal completely defines the different possibilities of displacement of the atoms within the crystallographic structure. The origin of the sliding planes lies in the contact between certain atoms of the crystal which generates, under stress, preferential directions of displacement. The sliding of the atoms along the sliding planes generates dislocations within the material. As with dislocations, there are different types of interaction between the sliding systems. These mechanisms at the microscopic scale largely describe the origins of the hardening of matter.

The first particularity of a monocrystalline law is in the use of the Schmid tensor to project the tensors of the stresses in the resolved shear stress.The Schmid tensor is determined from the normal to the slip plane and the direction of the slip. The second particularity lies in the introduction of an interaction matrix which weigths hardening according to the type of interaction considered. The last particularity is the introduction of the orientation of the crystal material for the elastic and the plastic modelization.

The behaviour is described by a standard decomposition of the strain \(\underline{\varepsilon}^{\mathrm{to}}\) in an elastic and a viscoplastic component, respectively denoted \(\underline{\varepsilon}^{\mathrm{el}}\) and \(\underline{\varepsilon}^{\mathrm{vis}}\):

\[ \underline{\varepsilon}^{\mathrm{to}}=\underline{\varepsilon}^{\mathrm{el}}+\underline{\varepsilon}^{\mathrm{vis}} \]

Elastic behaviour

The stress \(\underline{\sigma}\) is related to the the elastic strain \(\underline{\varepsilon}^{\mathrm{el}}\) by a the orthotropic elastic stiffness \(\underline{\underline{\mathbf{D}}}\):

\[ \underline{\sigma}= \underline{\underline{\mathbf{D}}}\,\colon\,\underline{\varepsilon}^{\mathrm{el}} \]

Viscoplastic behaviour

In the crystal frame, the viscoplastic strain rate is the summation of the slips along each slip systems, as follows:

\[ \underline{\dot{\varepsilon}}^{\mathrm{vis}}=\sum_{i=1}^{N}\dot{\gamma}_{i}\,\underline{m}_{i} \]

where \({\left({\underline{m}}_{i}\right)}_{i\in[1:N]}\) are the symmetric part of the orientation tensors, defined by:

\[ \underline{m}_{i}={{\displaystyle \frac{\displaystyle 1}{\displaystyle 2}}}\,{\left(\vec{n}_{i}\,\otimes\,\vec{b}_{i}+\vec{b}_{i}\,\otimes\,\vec{n}_{i}\right)} \]

with \(\vec{n}_{i}\) and \(\vec{b}_{i}\) being respectively the normal to the slip plane and the slip direction. \(\vec{n}_{i}\) and \(\vec{b}_{i}\) being orthogonal, the viscoplastic flow is incompressible 1.

The computation of the dissipated power yields:

\[ \underline{\sigma}\,\colon\,\underline{\dot{\varepsilon}}^{\mathrm{vis}}= \sum_{i=1}^{N}\dot{\gamma}_{i}\,\underline{\sigma}\,\colon\,\underline{m}_{i}= \sum_{i=1}^{N}\dot{\gamma}_{i}\,\tau_{i} \]

This equation shows that that the split rate is \(\dot{\gamma}_{i}\) is conjugated to the resolved shear stress \(\tau_{i}=\underline{\sigma}\,\colon\,\underline{m}_{i}\).

The Méric-Cailletaud behaviour is a scalar equivalent of the Norton-Hoff behaviour with isotropic and kinematic hardening along each slip plane, i.e. the split rate \(\dot{\gamma}_{i}\) is expressed as:

\[ \left\{ \begin{aligned} \dot{\gamma}_{i}&=\dot{p}_{i}\,\mathop{sgn}{\left(\tau_{i}-x_{i}\right)}\\ \dot{p}_{i}&=\left\langle{{\displaystyle \frac{\displaystyle \left|\tau_{i}-x_{i}\right|-R_{i}-\tau_{0}}{\displaystyle K}}}\right\rangle^n \end{aligned} \right. \qquad{(1)}\]

where \(p_{i}=\displaystyle\int_{t_{0}}^{t}\left|\dot{\gamma}_{i}\right|\,{{\mathrm{d}}}\,t\) is the equivalent viscoplastic slip.

The isotropic hardening rule couples the slip every systems as follows:

\[ R_{i}=Q\,\sum_{j=1}^{N}h_{ij}\,{\left(1-\exp{\left(-b\,p_{j}\right)}\right)} \qquad{(2)}\]

where \(h\) is the so-called interaction matrix

The kinematic hardening follows a scalar equivalent of the Armstrong-Frederick law:

\[ \left\{ \begin{aligned} x_{i}&=C\,\alpha_{i} \\ \dot{\alpha}_{i}&=\dot{\gamma}_{i}-D\,\alpha_{i}\,\dot{p}_{i} \end{aligned} \right. \qquad{(3)}\]

Integration algorithm

The behaviour will be integrated using an implicit scheme as described here.

Implicit system by direct discretization

A priori, The unknowns are the increments of the elastic strain \(\Delta\,\underline{\varepsilon}^{\mathrm{el}}\), of the plastic slips \({\left({\Delta\,\gamma}_{i}\right)}_{i\in[1:N]}\), of the equivalent plastic slips \({\left({\Delta\,p}_{i}\right)}_{i\in[1:N]}\) and of the back-strains \({\left({\Delta\,\alpha}_{i}\right)}_{i\in[1:N]}\). After a straightforward discretization, the following system of non equations are to be solved:

\[ \left\{ \begin{aligned} f_{\underline{\varepsilon}^{\mathrm{el}}} &= \Delta\,\underline{\varepsilon}^{\mathrm{el}}-\Delta\,\underline{\varepsilon}^{\mathrm{to}}+\sum_{i=1}^{N}\Delta\,\gamma_{i}\,\underline{m}_{i}&=0 \\ f_{\gamma_{i}} &= \Delta\,\gamma_{i}-\Delta\,p_{i}\,\mathop{sgn}{\left({\left.\tau_{i}\right|_{t+\theta\,\Delta\,t}}-{\left.x_{i}\right|_{t+\theta\,\Delta\,t}}\right)}&=0 \\ f_{p_{i}} &= \Delta\,p_{i}-\Delta\,t\,\left\langle{{\displaystyle \frac{\displaystyle \left|{\left.\tau_{i}\right|_{t+\theta\,\Delta\,t}}-{\left.x_{i}\right|_{t+\theta\,\Delta\,t}}\right|-{\left.R_{i}\right|_{t+\theta\,\Delta\,t}}-\tau_{0}}{\displaystyle K}}}\right\rangle^n &=0\\ f_{\alpha_{i}}&= \Delta\,\alpha_{i}-\Delta\,\gamma_{i}+D\,{\left.\alpha_{i}\right|_{t+\theta\,\Delta\,t}}\,\Delta\,p_{i}&=0 \end{aligned} \right. \qquad{(4)}\]

where :

This number of unknowns of System (4) is egal to \(6+3\,N_{ss}\) where \(N_{ss}\) is the number of slip systems and \(6\) is the number of component of the elastic strain.

Reduction of the number of unknowns

We now show how to reduce the size of this system to \(6+N_{ss}\).

Notes

Reducing the number of unknowns has two main impacts:

First, the relationship between \(\Delta\,p_{i}\) and \(\Delta\,\gamma_{i}\) is trivial:

\[ \Delta\,p_{i}=\left|\Delta\,\gamma_{i}\right| \]

One may choose one of them and eliminate the other for the system. In the following, we keep \(\Delta\,\gamma_{i}\).

It shall be noted that:

Second, \(f_{\alpha_{i}}\) can be used to express \(\Delta\,\alpha_{i}\) as a function of \(\Delta\,p_{i}\) and \(\Delta\,\gamma_{i}\) :

\[ \begin{aligned} \Delta\,\alpha_{i}&= {{\displaystyle \frac{\displaystyle \Delta\,\gamma_{i}-D\,{\left.\alpha_{i}\right|_{t}}\,\Delta\,p_{i}}{\displaystyle 1+D\,\theta\,\Delta\,p_{i}}}}= {{\displaystyle \frac{\displaystyle \Delta\,\gamma_{i}-D\,{\left.\alpha_{i}\right|_{t}}\,\left|\Delta\,\gamma_{i}\right|}{\displaystyle 1+D\,\theta\,\left|\Delta\,\gamma_{i}\right|}}}\\ &={\left(1-D\,{\left.\alpha_{i}\right|_{t}}\,\mathop{sgn}{\left(\Delta\,\gamma_{i}\right)}\right)}\,{{\displaystyle \frac{\displaystyle \Delta\,\gamma_{i}}{\displaystyle 1+D\,\theta\,\mathop{sgn}{\left(\Delta\,\gamma_{i}\right)}\,\Delta\,\gamma_{i}}}} \end{aligned} \qquad{(5)}\]

Finally, the implicit system to be solved is:

\[ \left\{ \begin{aligned} f_{\underline{\varepsilon}^{\mathrm{el}}} &= \Delta\,\underline{\varepsilon}^{\mathrm{el}}-\Delta\,\underline{\varepsilon}^{\mathrm{to}}+\sum_{i=1}^{N}\Delta\,\gamma_{i}\,\underline{m}_{i}&=0 \\ f_{\gamma_{i}}&=\Delta\,\gamma_{i}-\Delta\,t\,v{\left(f\right)}\,\mathop{sgn}{\left(\tau_e\right)} \end{aligned} \right. \qquad{(6)}\]

with:

The latter notations have been introduced to ease the analytical computation of the jacobian, see Section 4.1.

Implementation using a numerical jacobian

Choice of the domain specific language

The implementation begins with the choice of the Implicit domain specific language (dsl):

@DSL Implicit;

Note that this dsl automatically declares the elastic strain eel as a state variable.

Metadata

The following code declares the name of the behaviour, the names of the authors, and the date.

@Behaviour MericCailletaudSingleCrystalViscoPlasticityNumericalJacobian;
@Author Thomas Helfer, Alexandre Bourceret;
@Date 17 / 10 / 2019;

Supported modelling hypothesis

This behaviour is only valid in \(3D\). The following line restricts the behaviour to be only usable in \(3D\):

@ModellingHypothesis Tridimensional;

Material symmetry

The behaviour describes an orthotropic material:

@OrthotropicBehaviour;

Note

As the behaviour is only valid in \(3D\), there is no need to specify any orthotropic axises convention (see the @OrthotropicBehaviour keyword for details).

Numerical parameters

The following lines declare that we want to use a standard Newton-Raphson algorithm with a numerically evaluated jacobian. The perturbation value used to evaluate the jacobian is chosen equal to \(10^{-7}\) which is a reasonnable value.

@Algorithm NewtonRaphson_NumericalJacobian;
@PerturbationValueForNumericalJacobianComputation 1.e-7;

The stopping criterion is chosen low, to ensure the quality of the consistent tangent operator (the default value, \(10^{-8}\) is enough to ensure a good estimation of the state variable evolution, but is not enough to have a proper estimation of the consistent tangent operator):

@Epsilon 1e-14;

We explicit state that a fully implicit integration will be used by default:

@Theta 1;

This value can be changed at runtime by modifying the theta parameter.

Usage of the StandardElasticity brick

To implement this behaviour, we will use the StandardElasticity brick which provides:

This behaviour brick is fully described here.

The usage of the StandardElasticity is declared as follows:

@Brick StandardElasticity{
  young_modulus1 : 208000,
  young_modulus2 : 208000,
  young_modulus3 : 208000,
  poisson_ratio12 : 0.3,
  poisson_ratio23 : 0.3,
  poisson_ratio13 : 0.3,
  shear_modulus12 : 80000,
  shear_modulus23 : 80000,
  shear_modulus13 : 80000
};

Note

Here, we chose to declare the elastic material properties as part of the brick declaration. This pratice has been introduced in TFEL-3.2 with the development of the StandardElastoViscoPlasticitybrick. The material properties can also be computed using a formula or an external MFront files.

The elastic material properties can also be introduced by:

The declaration of the elastic material properties automatically defines the variables D and D_tdt which respectively holds the stiffness tensor at the middle of the time step (at \(t+\theta\,\Delta\,t\) and the stiffness at the end of the time step (at \(t+\Delta\,t\).

Definition of the crystal structure, the slip systems and the interaction matrix

The following lines, based on the TFELNumodis library introduced in TFEL 3.1.0 defines the the crystal structure, the slip systems and the interaction matrix:

@CrystalStructure FCC;
@SlidingSystem<0, 1, -1>{1, 1, 1};
@InteractionMatrix{1, 1, 0.6, 1.8, 1.6, 12.3, 1.6};

Those keywords are fully documented on this page. We highly recommend that the user take the time to understandand how they work.

In this particular case, the family <0, 1, -1>{1, 1, 1} generates \(12\) slips systems by symmetry. The generated slip systems and their associated indexes can be retrieved by the mfront-query tool:

$ mfront-query MericCailletaudSingleCrystalViscoPlasticityNumericalJacobian.mfront --slip-systems-by-index
- 0: [0,1,-1](1,1,1)
- 1: [1,0,-1](1,1,1)
- 2: [1,-1,0](1,1,1)
- 3: [0,1,1](1,1,-1)
- 4: [1,0,1](1,1,-1)
- 5: [1,-1,0](1,1,-1)
- 6: [0,1,-1](1,-1,-1)
- 7: [1,0,1](1,-1,-1)
- 8: [1,1,0](1,-1,-1)
- 9: [0,1,1](1,-1,1)
- 10: [1,0,-1](1,-1,1)
- 11: [1,1,0](1,-1,1)

The interation matrix, which is non symmetric, has \(7\) independent coefficients. The precise structure of this interaction matrix can be retrieved thank to the mfront-query tool as follows:

$ mfront-query MericCailletaudSingleCrystalViscoPlasticityNumericalJacobian.mfront --interaction-matrix
| 0 1 1 2 3 4 5 6 6 2 4 3 |
| 1 0 1 3 2 4 4 2 3 6 5 6 |
| 1 1 0 6 6 5 4 3 2 3 4 2 |
| 2 3 4 0 1 1 2 4 3 5 6 6 |
| 3 2 4 1 0 1 6 5 6 4 2 3 |
| 6 6 5 1 1 0 3 4 2 4 3 2 |
| 5 6 6 2 4 3 0 1 1 2 3 4 |
| 4 2 3 6 5 6 1 0 1 3 2 4 |
| 4 3 2 3 4 2 1 1 0 6 6 5 |
| 2 4 3 5 6 6 2 3 4 0 1 1 |
| 6 5 6 4 2 3 3 2 4 1 0 1 |
| 3 4 2 4 3 2 6 6 5 1 1 0 |
with:
- coefficient '0': 1
- coefficient '1': 1
- coefficient '2': 0.6
- coefficient '3': 1.8
- coefficient '4': 1.6
- coefficient '5': 12.3
- coefficient '6': 1.6

Those instructions also automatically defines :

Material parameters

The following block of code defines the various material parameters used in the constitutive equations associated with the plastic slips:

@Parameter n = 10.0;
@Parameter K = 25.;
@Parameter tau0 = 66.62;
@Parameter Q = 11.43;
@Parameter b = 2.1;
@Parameter d = 494.0;
@Parameter C = 14363;

Integration variables, state variables and auxiliary state variables

As described earlier (see Section 2), the viscoplastic slips \({\left({\gamma}_{i}\right)}_{i\in[1:N]}\) are declared as integration variables as follows:

@IntegrationVariable strain g[Nss];
g.setEntryName("ViscoplasticSlip");

As discussed before, declaring the viscoplastic slips as state variables would save their values from one step to the other which can be convenient for debugging and/or post-processing.

The equivalent viscoplastic slips and the back-strains are declared as auxiliary state variables:

@AuxiliaryStateVariable strain p[Nss];
p.setEntryName("EquivalentViscoplasticSlip");

@AuxiliaryStateVariable strain a[Nss];
a.setEntryName("BackStrain");

Implicit system

The @Integrator block allows the definition of the implicit system. We divided it into three sections:

Preamble

@Integrator {
  using size_type = unsigned short;
  const auto &ss =
      MericCailletaudSingleCrystalViscoPlasticityNumericalJacobianSlipSystems<
          real>::getSlipSystems();
  const auto& m = ss.him;

The first line defines a type alias: after this size_type is a short hand for the unsigned short integer type used as the index type by loops on the slip systems.

The second line retrieves the uniq instance of the MericCailletaudSingleCrystalViscoPlasticityNumericalJacobianSlipSystems class. The const keywords means that this variable is immutable. The auto keyword means that the type of the ss variable is deduced by the compiler. The ampersand character & means that ss is a reference, i.e. the object returned by the getSlipSystems method is not copied.

The object referenced by thess variable contains two data members:

The last line defines m as an immutable reference the the interaction matrix.

Precomputation of the exponentials

In order to precompute the exponentials appearing in the isotropic hardening of each slip systems, we first compute declare an array of size Nss called exp_bp. We then loop over each slip systems.

  // precomputing the exponentials used to compute the isotropic hardening of
  // each slip systems
  real exp_bp[Nss];
  for (size_type i = 0; i != Nss; ++i) {
      const auto p_ = p[i] + theta * abs(dg[i]);
      exp_bp[i] = exp(-b * p_);
  }

Definition of the implicit equations

Befor defining the implicit equations, it is important to remember a few conventions of the Implicit DSL and of the StandardElasticity brick:

Thus, the evaluation of the implicit equations are mostly a loop over the slip systems which is meant to update feel and define the implicit equation for the considered system.

This loop has three main parts:

  1. Computing the yield stress by taking into account the contributions of the other slip systems (see Equation (2)).
  2. Computing the back-strain increment and the back stress using Equations (5) and (3).
  3. Computing the plastic slip rate using the resolved shear stress (see Equation (1)).

Finally, the implementation of the implicit equations closely mimics System (6).

  // loop over the slip systems
  for (size_type i = 0; i != Nss; ++i) {
    // isostropic hardening
    auto r = tau0;
    for (size_type j = 0; j != Nss; ++j) {
      r += Q * m(i, j) * (1 - exp_bp[j]);
    }
    // back strain increment and kinematic hardening
    const auto da =  //
        (dg[i] - d * a[i] * abs(dg[i])) / (1 + theta * d * abs(dg[i]));
    const auto x = C * (a[i] + theta * da);
    // resolved shear stress
    const auto tau = sig | ss.mus[i];
    const auto f = max(abs(tau - x) - r, stress(0));
    const auto sgn = tau - x > 0 ? 1 : -1;
    fg[i] -= dt * pow(f / K, n) * sgn;
    feel += dg[i] * ss.mus[i];
  }
}

Auxiliary state variables update

Once the Newton-Raphson algorithm converged, one need to update the auxiliary state variables as follows:

@UpdateAuxiliaryStateVariables {
  using size_type = unsigned short;
  for (size_type i = 0; i != Nss; ++i) {
    p[i] += abs(dg[i]);
    const auto da =  //
        (dg[i] - d * a[i] * abs(dg[i])) / (1 + theta * d * abs(dg[i]));
    a[i] += da;
  }
}

Improving the robustness of the Newton-Raphson algorithm

When the Norton exponent \(n\) is reasonnable, the standard Newton-Raphson algorithm works pretty good. However, in practice, this exponent is usually very high, typically between \(70\) and \(100\) which almost imposes \(f=\left|\tau_e\right|-R_{i}-\tau_0\) to be equal or lower to \(K\).

One simple trick to handle this condition is to reject Newton steps that would lead to values of \(f\) too high. This can simply be done by inserting the following test after the definition of f:

    if (f > 1.1 * K) {
      return false;
    }

Implementation with an analytical jacobian

The implementation of the behaviour with an analytical jacobian is quite similar.

Jacobian

To solve System (6), one must compute its jacobian \(J\), which can be decomposed by blocks:

\[ J= \begin{pmatrix} {\displaystyle \frac{\displaystyle \partial f_{\underline{\varepsilon}^{\mathrm{el}}}}{\displaystyle \partial \Delta\,\underline{\varepsilon}^{\mathrm{el}}}} & \dots& {\displaystyle \frac{\displaystyle \partial f_{\underline{\varepsilon}^{\mathrm{el}}}}{\displaystyle \partial \Delta\,\gamma_{i}}} & \dots& {\displaystyle \frac{\displaystyle \partial f_{\underline{\varepsilon}^{\mathrm{el}}}}{\displaystyle \partial \Delta\,\gamma_{j}}} & \dots \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ {\displaystyle \frac{\displaystyle \partial f_{\gamma_{i}}}{\displaystyle \partial \Delta\,\underline{\varepsilon}^{\mathrm{el}}}} & \dots& {\displaystyle \frac{\displaystyle \partial f_{\gamma_{i}}}{\displaystyle \partial \Delta\,\gamma_{i}}} & \dots& {\displaystyle \frac{\displaystyle \partial f_{\gamma_{i}}}{\displaystyle \partial \Delta\,\gamma_{j}}} & \dots \\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ {\displaystyle \frac{\displaystyle \partial f_{\gamma_{j}}}{\displaystyle \partial \Delta\,\underline{\varepsilon}^{\mathrm{el}}}} & \dots& {\displaystyle \frac{\displaystyle \partial f_{\gamma_{j}}}{\displaystyle \partial \Delta\,\gamma_{i}}} & \dots& {\displaystyle \frac{\displaystyle \partial f_{\gamma_{j}}}{\displaystyle \partial \Delta\,\gamma_{j}}} & \dots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ \end{pmatrix} \]

\({\displaystyle \frac{\displaystyle \partial f_{\underline{\varepsilon}^{\mathrm{el}}}}{\displaystyle \partial \Delta\,\underline{\varepsilon}^{\mathrm{el}}}}\) and \({\displaystyle \frac{\displaystyle \partial f_{\underline{\varepsilon}^{\mathrm{el}}}}{\displaystyle \partial \Delta\,\gamma_{i}}}\) are trivial:

\[ \left\{ \begin{aligned} {\displaystyle \frac{\displaystyle \partial f_{\underline{\varepsilon}^{\mathrm{el}}}}{\displaystyle \partial \Delta\,\underline{\varepsilon}^{\mathrm{el}}}}&=\underline{\underline{\mathbf{I}}}\\ {\displaystyle \frac{\displaystyle \partial f_{\underline{\varepsilon}^{\mathrm{el}}}}{\displaystyle \partial \Delta\,\gamma_{i}}}&=\underline{m}_{i}\\ {\displaystyle \frac{\displaystyle \partial f_{\underline{\varepsilon}^{\mathrm{el}}}}{\displaystyle \partial \Delta\,\gamma_{j}}}&=\underline{m}_{j}\\ \end{aligned} \right. \]

The other derivatives are tedious to compute, but not really difficult: \[ \left\{ \begin{aligned} {\displaystyle \frac{\displaystyle \partial f_{\gamma_{i}}}{\displaystyle \partial \Delta\,\underline{\varepsilon}^{\mathrm{el}}}} &= -\Delta\,t{\displaystyle \frac{\displaystyle \partial v}{\displaystyle \partial f}}\,{\displaystyle \frac{\displaystyle \partial f}{\displaystyle \partial \tau_e}}\,{\displaystyle \frac{\displaystyle \partial \tau_e}{\displaystyle \partial {\left.\tau_{i}\right|_{t+\theta\,\Delta\,t}}}}\,{\displaystyle \frac{\displaystyle \partial {\left.\tau_{i}\right|_{t+\theta\,\Delta\,t}}}{\displaystyle \partial {\left.\underline{\sigma}\right|_{t+\theta\,\Delta\,t}}}}\,\colon\,{\displaystyle \frac{\displaystyle \partial {\left.\underline{\sigma}\right|_{t+\theta\,\Delta\,t}}}{\displaystyle \partial \Delta\,\underline{\varepsilon}^{\mathrm{el}}}}\,\mathop{sgn}{\left(\tau_e\right)}\\ &= -\Delta\,t{\displaystyle \frac{\displaystyle \partial v}{\displaystyle \partial f}}\,\theta\,\underline{m}_{i}\,\colon\,\underline{\underline{\mathbf{D}}}\\ {\displaystyle \frac{\displaystyle \partial f_{\gamma_{i}}}{\displaystyle \partial \Delta\,\gamma_{i}}} &= 1-\Delta\,t{\displaystyle \frac{\displaystyle \partial v}{\displaystyle \partial f}}\, \left[ {\displaystyle \frac{\displaystyle \partial f}{\displaystyle \partial \tau_e}}\,{\displaystyle \frac{\displaystyle \partial \tau_e}{\displaystyle \partial {\left.x_{i}\right|_{t+\theta\,\Delta\,t}}}}\,{\displaystyle \frac{\displaystyle \partial {\left.x_{i}\right|_{t+\theta\,\Delta\,t}}}{\displaystyle \partial {\left.\alpha_{i}\right|_{t+\theta\,\Delta\,t}}}}\,{\displaystyle \frac{\displaystyle \partial {\left.\alpha_{i}\right|_{t+\theta\,\Delta\,t}}}{\displaystyle \partial \Delta\,\alpha_{i}}}\,{\displaystyle \frac{\displaystyle \partial \Delta\,\alpha_{i}}{\displaystyle \partial \Delta\,\gamma_{i}}} + {\displaystyle \frac{\displaystyle \partial f}{\displaystyle \partial R_{i}}}\,{\displaystyle \frac{\displaystyle \partial R_{i}}{\displaystyle \partial \Delta\,\gamma_{i}}} \right]\,\mathop{sgn}{\left(\tau_e\right)}\\ &= 1+\Delta\,t{\displaystyle \frac{\displaystyle \partial v}{\displaystyle \partial f}}\, \left[ C\,\theta\,{\displaystyle \frac{\displaystyle \partial \Delta\,\alpha_{i}}{\displaystyle \partial \Delta\,\gamma_{i}}} + \mathop{sgn}{\left(\tau_e\right)}\,{\displaystyle \frac{\displaystyle \partial R_{i}}{\displaystyle \partial \Delta\,\gamma_{i}}} \right]\\ {\displaystyle \frac{\displaystyle \partial f_{\gamma_{i}}}{\displaystyle \partial \Delta\,\gamma_{j}}} &= \Delta\,t{\displaystyle \frac{\displaystyle \partial v}{\displaystyle \partial f}}\,{\displaystyle \frac{\displaystyle \partial R_{i}}{\displaystyle \partial \Delta\,\gamma_{j}}}\,\mathop{sgn}{\left(\tau_e\right)} \end{aligned} \right. \]

with:

Modification of the previous implementation

From the previous file, one must:

Again, it is important to recall the convention of the Implicit DSL concerning the initialization of the jacobian is to set it to identity.

The new @Integrator block is now:

@Integrator {
  using size_type = unsigned short;
  constexpr const auto eeps = 1.e-12;
  const auto seps = eeps * D(0, 0);
  const auto& ss = //
      MericCailletaudSingleCrystalViscoPlasticitySlipSystems<real>::getSlipSystems();
  const auto& m = ss.him;
  real exp_bp[Nss];
  for (size_type i = 0; i != Nss; ++i) {
      const auto p_ = p[i] + theta * abs(dg[i]);
      exp_bp[i] = exp(-b * p_);
  }
  for (size_type i = 0; i != Nss; ++i) {
    const auto tau = sig | ss.mus[i];
    auto r = tau0;
    for (size_type j = 0; j != Nss; ++j) {
      r += Q * m(i, j) * (1 - exp_bp[j]);
    }
    const auto da =  //
        (dg[i] - d * a[i] * abs(dg[i])) / (1 + theta * d * abs(dg[i]));
    const auto x = C * (a[i] + theta * da);
    const auto f = max(abs(tau - x) - r, stress(0));
    if (f > 1.1 * K) {
      return false;
    }
    const auto sgn = tau - x > 0 ? 1 : -1;
    // elasticity
    feel += dg[i] * ss.mus[i];
    dfeel_ddg(i) = ss.mus[i];
    // viscoplasticity
    const auto v = pow(f / K, n);
    const auto dv = n * v / (max(f, seps));
    fg[i] -= dt * pow(f / K, n) * sgn;
    dfg_ddeel(i) = -dt * dv * (ss.mus[i] | D);
    const auto sgn_gi = dg(i) > 0 ? 1 : -1;
    const auto dda_ddg =
        (1 - d * a[i] * sgn_gi) / (power<2>(1 + theta * d * abs(dg[i])));
    dfg_ddg(i, i) += dt * dv * C * theta * dda_ddg;
    for (size_type j = 0; j != Nss; ++j) {
      const auto sgn_gj = dg(j) > 0 ? 1 : -1;
      const auto dr = Q * m(i, j) * theta * b * exp_bp[j] * sgn_gj;
      dfg_ddg(i, j) += dt * dv * dr * sgn;
    }
  }
}

Benchmarks

Table 1: Results of MericCailletaudSingleCrystalViscoPlasticity profiling : 8msecs 600musecs 753nsecs
Integrator 8msecs 82musecs 148nsecs (8082148 ns)
Integrator::ComputeThermodynamicForces 512musecs 422nsecs (512422 ns)
Integrator::ComputeFdF 2msecs 177musecs 565nsecs (2177565 ns)
Integrator::TinyMatrixSolve 3msecs 846musecs 171nsecs (3846171 ns)
ComputeFinalThermodynamicForces 25musecs 395nsecs (25395 ns)
ComputeTangentOperator 334musecs 361nsecs (334361 ns)
UpdateAuxiliaryStateVariables 23musecs 852nsecs (23852 ns)
Table 2: Results of MericCailletaudSingleCrystalViscoPlasticityNumericalJacobian profiling : 69msecs 631musecs 952nsecs
Integrator 69msecs 277musecs 664nsecs (69277664 ns)
Integrator::ComputeThermodynamicForces 12msecs 83musecs 980nsecs (12083980 ns)
Integrator::ComputeFdF 30msecs 512musecs 471nsecs (30512471 ns)
Integrator::TinyMatrixSolve 2msecs 538musecs 618nsecs (2538618 ns)
ComputeFinalThermodynamicForces 16musecs 989nsecs (16989 ns)
ComputeTangentOperator 225musecs 267nsecs (225267 ns)
UpdateAuxiliaryStateVariables 15musecs 801nsecs (15801 ns)

Extenstion to finite strain

To extend the implementation to finite strain, we will use the FiniteStrainSingleCrystal brick which is described here.

In pratice, thanks to this brick, only a very limited number of changes are required:

Applications

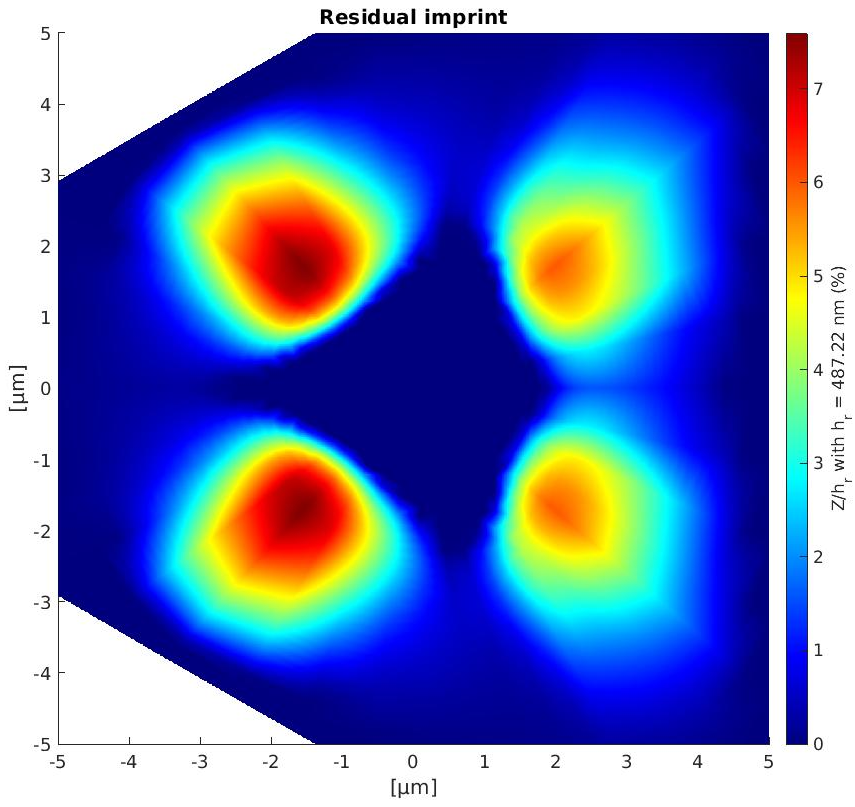
Simulated residual topography after a Berkovich indentation test in a single crystal. The values are normalized by the residual indentation depth h_{r}
Figure 1: Simulated residual topography after a Berkovich indentation test in a single crystal. The values are normalized by the residual indentation depth \(h_{r}\)

This study has been conducted as part of the the PhD thesis of A.Bourceret (FEMTO) supervised by A.Lejeune, Y.Gaillard and F.Richard (FEMTO). It deals with the modelling of a Berkovich nanoindentation test on a copper sample which is described by the Meric-Cailletaud single crystal law at finite strain.

The imposed displacement of the berkovich indenter to a maximum value of \(500\,nm\). For this simulation the material parameters identified copper by Méric et al were used [1].

The finite element model based contains \(4.10^4\) elements for the geometric description of the copper sample and the Berkovich indenter. This model is treated by the Ansys finite element solver. The results of this simulation are reported on Figure 1 which represents the simulated residual topography.

Usage in code_aster

Based on this tutorial, Nicolò Grilli (University of Bristol) published a series of three videos showing in details how to make single and polycrystal simulations with MFront and code_aster:

The series adresses several advanced topics regarding the interface between code_ater and MFront:

which can be very handy for a lot of users.

References

1.
Méric, L. and Cailletaud, Georges. Single crystal modelling for structural calculations. Journal of Engineering Material and Technology. January 1991. Vol. 113, p. 171–182.