This document gives some insights on how a user may extend the StandardElastoViscoPlasticity brick by adding a new stress criterion.

The StandardElastoViscoPlasticity brick is fully described here.

Introducing a new stress criterion in the StandardElastoViscoPlasticity brick has two main steps:

Note

This tutorial only covers isotropic stress criteria. Orthotropic stress criteria requires to take care of the orthotropic axes convention.

See the documentation of the @OrthotropicBehaviour keyword for details:

mfront --help-keyword=Implicit:@OrthotropicBehaviour

1 Extending the TFEL/Material library

1.1 Template files

We recommend that you use the following template files:

The first file declares:

The second file give a skeleton required to implement those three functions.

Implementing a new stress criterion boils down to the following steps:

  1. Rename those file to explicitly indicate the name of the stress criterion.
  2. Replace the following strings by the appropriate values as described below:
  1. Implement the three previous functions
  2. Test your implementation in MFront and MTest (or your favorite solver).

1.2 Creating a proper working directory for the example of the Green criterion

In this paragraph, we detail Steps 1 and 2. for the case of the Green criterion (see [1]) which will be used as an illustrative example throughout this document. We describe all those steps in details and finally gives a shell script that automates the whole process for LiNuX users. When providing command line examples, we assume that the shell is bash.

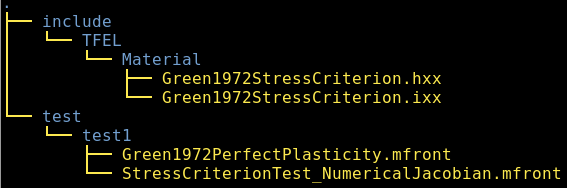
The header files StressCriterionTemplate.hxx and StressCriterionTemplate.ixx are placed in a subdirectory called include/TFEL/Material and renamed respectively Green1972StressCriterion.hxx and Green1972StressCriterion.ixx.

The MFront template files must be copied in the working directory and renamed appropriatly.

This can be done by taping the following commands in the terminal (under LiNuX or Mac Os):

$ mkdir -p include/TFEL/Material
$ mkdir -p tests/test1
$ mv StressCriterionTemplate.hxx \
     include/TFEL/Material/Green1972StressCriterion.hxx
$ mv StressCriterionTemplate.ixx \
     include/TFEL/Material/Green1972StressCriterion.ixx
$ mv StressCriterionTest.mfront \
     tests/test1/Green1972PerfectPlasticity.mfront
$ mv StressCriterionTest_NumericalJacobian.mfront \
     tests/test1/Green1972PerfectPlasticity_NumericalJacobian.mfront

The working directory is thus organized as follows:

In all those files, we now replace

You may use your favourite text-editor to do this or use the following command (for LiNuX users) :

for f in $(find . -type f);                                        \
do sed -i                                                          \
  -e 's|__Author__|Thomas Helfer, Jérémy Hure, Mohamed Shokeir|g;' \
  -e 's|__Date__|24/03/2020|g;'                                    \
  -e 's|__StressCriterionName__|Green1972|g;'                      \
  -e 's|__STRESS_CRITERION_NAME__|GREEN_1972|g' $f ;               \
done

All those steps are summarized in the following script, which can be downloaded here.

In conclusion, a recommended for starting the development of the a new stress criterion is to download the previous script, modify appropriately the first lines to match your need and run it.

Note

At this stage, you shall already be able to verify that the provided MFront implementations barely compiles by typing in the tests/test1 directory:

mfront -I $(pwd)/../../include --obuild \
       --interface=generic        \
       Green1972PerfectPlasticity.mfront

Note the -I $(pwd)/../../include flags which allows MFront to find the header files implementing the stress criterion (In bash, $(pwd) return the current directory).

1.3 Implementing the Green 1972 stress criterion

In this paragraph, we detail all the steps required to implement the Green 1972 stress criterion (see [1] for the original paper, [2] for the paper that we follow for this work).

The green stress criterion is defined by:

\[ \sigma_{\mathrm{eq}}=\sqrt{{{\displaystyle \frac{\displaystyle 3}{\displaystyle 2}}}\,C\,\underline{s}\,\colon\,\underline{s}+F\,{\mathrm{tr}{\left(\underline{\sigma}\right)}}^{2}} \]

where \(C\) and \(F\) are two material properties.

The implementation of a perfect plasticity in pure MFront is detailed in an entry of the MFront gallery:

https://thelfer.github.io/tfel/web/greenplasticity.html

In a new directory, we just follow the steps given by the previous paragraph:

wget https://thelfer.github.io/tfel/web/scripts/generate.sh
chmod +x generate.sh
./generate.sh

1.3.1 Modifying the Green1972StressCriterionParameters data structure

The Green1972StressCriterionParameters data structure, declared in Green1972StressCriterion.hxx, must contain the values of the \(F\) and \(G\) material parameters.

We modify it as follows:

template <typename StressStensor>
struct Green1972StressCriterionParameters {
  //! a simple alias
  using real = Green1972BaseType<StressStensor>;
  //! \brief \f$F\f$ material property
  real F;
  //! \brief \f$C\f$ material property
  real C;
};  // end of struct Green1972StressCriterionParameters

The output stream operator must now be implemented in the Green1972StressCriterion.ixx file:

template <typename StressStensor>
std::ostream &operator<<(std::ostream &os,
                         const Green1972StressCriterionParameters<StressStensor> &p) {
  os << "{F: " << p.F << ", C: " << p.C << "}";
  return os;
} // end of operator<<

This operator is useful when compiling MFront files in debug mode.

1.3.2 Implementing the computeGreen1972Stress function

The computeGreen1972Stress function is implemented in the Green1972StressCriterion.ixx file.

Following the definition of the equivalent stress, this implementation is straightforward:

template <typename StressStensor>
Green1972StressType<StressStensor> computeGreen1972Stress(
    const StressStensor& sig,
    const Green1972StressCriterionParameters<StressStensor>& p,
    const Green1972StressType<StressStensor> seps) {
  const auto s  = deviator(sig);
  const auto tr = trace(sig);
  return std::sqrt(3 * (p.C) * (s | s) / 2 + //
                   (p.F) * tr * tr);
}  // end of computeGreen1972YieldStress

Note

It is worth trying to recompile the MFront file at this stage to see if one did not introduce any error in the C++ code.

1.3.3 Implementing the computeGreen1972StressNormal function

This function computes the equivalent stress and its normal. The expression of the normal is:

\[ \underline{n} = {\displaystyle \frac{\displaystyle \partial f}{\displaystyle \partial \underline{\sigma}}} = {{\displaystyle \frac{\displaystyle 1}{\displaystyle \sigma_{\mathrm{eq}}}}}\,{\left({{\displaystyle \frac{\displaystyle 3}{\displaystyle 2}}}\,C\,\underline{s}+F\,{\mathrm{tr}{\left(\underline{\sigma}\right)}}\,\underline{I}\right)} \]

This expression introduces the inverse of the equivalent stress which may lead to numerical troubles. To avoid those issues, a numerical threshold is introduced in the computation of the inverse in our implementation:

template <typename StressStensor>
std::tuple<Green1972StressType<StressStensor>,
           Green1972StressNormalType<StressStensor>>
computeGreen1972StressNormal(
    const StressStensor& sig,
    const Green1972StressCriterionParameters<StressStensor>& p,
    const Green1972StressType<StressStensor> seps) {
  constexpr const auto id = Green1972StressNormalType<StressStensor>::Id();
  const auto s = deviator(sig);
  const auto tr = trace(sig);
  const auto seq = std::sqrt(3 * (p.C) * (s | s) / 2 + //
                             (p.F) * tr * tr);
  const auto iseq = 1 / (std::max(seq, seps));
  const auto n = eval(iseq * ((3 * (p.C)) / 2 * s + //
                              (p.F) * tr * id));
  return {seq, n};
}  // end of computeGreen1972StressNormal

Note

At this stage, the MFront implementation based on a numerical jacobian could be fully functional if one modifies the @InitLocalVarialbes block to initialize the parameters of stress criterion.

1.3.4 Implementing the computeGreen1972StressSecondDerivative function

This function computes the equivalent stress, its normal and the derivative of the normal (i.e. the second derivative of the equivalent stress).

The expression of the derivative of the normal is:

\[ {\displaystyle \frac{\displaystyle \partial \underline{n}}{\displaystyle \partial \sigma}}={{\displaystyle \frac{\displaystyle 1}{\displaystyle \sigma_{\mathrm{eq}}}}}\,{\left({{\displaystyle \frac{\displaystyle 3}{\displaystyle 2}}}\,C\,\,\underline{\underline{\mathbf{I}}}+{\left(F-{\left({{\displaystyle \frac{\displaystyle C}{\displaystyle 2}}}\right)}\right)}\,\underline{I}\,\otimes\,\underline{I}-\underline{n}\,\otimes\,\underline{n}\right)} \]

The implementation of the computeGreen1972StressSecondDerivative function is then:

template <typename StressStensor>
std::tuple<Green1972StressType<StressStensor>,
           Green1972StressNormalType<StressStensor>,
           Green1972StressSecondDerivativeType<StressStensor>>
computeGreen1972StressSecondDerivative(
    const StressStensor& sig,
    const Green1972StressCriterionParameters<StressStensor>& p,
    const Green1972StressType<StressStensor> seps) {
  // a simple alias to the underlying numeric type
  using real = Green1972BaseType<StressStensor>;
  // space dimension deduced from the type of the stress tensor
  constexpr const auto N = tfel::math::StensorTraits<StressStensor>::dime;                           
  constexpr const auto id = Green1972StressNormalType<StressStensor>::Id();
  constexpr const auto id4 = tfel::math::st2tost2<N,real>::Id();
  const auto s = deviator(sig);
  const auto tr = trace(sig);
  const auto seq = std::sqrt(3 * (p.C) * (s | s) / 2 + //
                             (p.F) * tr * tr);
  const auto iseq = 1 / (std::max(seq, seps));
  const auto n = iseq * (3 * (p.C) * s / 2 + //
                         (p.F) * tr * id);
  const auto dn =
      ((3 * p.C / 2) * id4 + (p.F - p.C / 2) * (id ^ id) - (n ^ n)) *
      iseq;
  return {seq, n, dn};
}  // end of computeGreen1972SecondDerivative

1.3.5 Modifying the MFront implementations

At this stage, the provided MFront implementations are almost working. Only the initializations of the parameters of the yield criterion is missing.

First, we define two parameters called F and C:

@Parameter C = 0.8;
C.setEntryName("GreenYieldCriterion_C");
@Parameter F = 0.2;
F.setEntryName("GreenYieldCriterion_F");

And then we use two parameters to initialize the parameters of the yield criterion in the @InitLocalVariables block:

@InitLocalVariables {
  // initialize the parameters from the material properties
  params.F = F;
  params.C = C;
  ...

1.3.6 Testing

At this stage, your implementations are fully functional. Go in the tests/test1 subdirectory and compile the examples with:

$ mfront -I $(pwd)/../../include --obuild --interface=generic \
         Green1972PerfectPlasticity.mfront              \
         Green1972PerfectPlasticity_NumericalJacobian.mfront

One may test it under a simple tensile test:

@Author Thomas Helfer, Jérémy Hure, Mohamed Shokeir;
@Date   25/03/2020;
@Description{
  A simple tensile test to check the implementation
  of a perfect plastic behaviour based of the Green
  criterion.
};

@MaximumNumberOfSubSteps 1;
@Behaviour<generic> 'src/libBehaviour.so' 'Green1972PerfectPlasticity';

// external state variables
@ExternalStateVariable 'Temperature' 293.15;

@ImposedStrain 'EXX' {
  0 : 0, 1 : 1.e-2
};

@Times{0, 1 in 10};

Note

The numerical jacobian version fails with this time discretization at the first time step because the jacobian is singular when the stress tensor is null in perfect plasticity, which happens in the first time step.

The implementation of the behaviour with analytic jacobian has a little trick in the definition of the df_ddp block to avoid this discrepancy.

In the numerical jacobian case, one solution is to add a small time step at the beginning, while still is the elastic domain.

This test allows checking that:

$ mfront -I $(pwd)/../../include --obuild --interface=generic \
         Green1972PerfectPlasticity.mfront              \
         --@CompareToNumericalJacobian=true             \
         --@PerturbationValueForNumericalJacobianComputation=1.e-8
$ mfront -I $(pwd)/../../include --obuild --interface=generic \
         Green1972PerfectPlasticity.mfront --debug
$ mtest Green1972PerfectPlasticity.mtest                   \
        --@CompareToNumericalTangentOperator=true          \
        --@NumericalTangentOperatorPerturbationValue=1.e-8 \
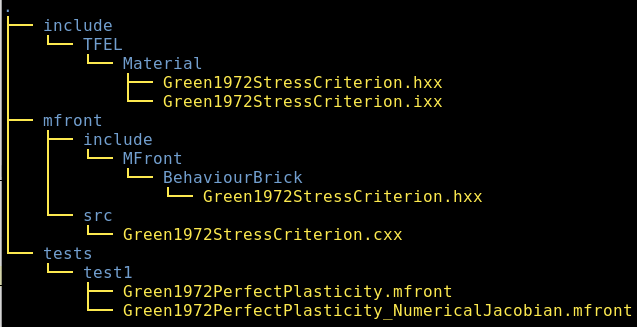
        --@TangentOperatorComparisonCriterium=1

2 Extending the TFELMFront library

2.1 Updating the working directory

We recommend that you use the following template files:

The first file must be copied in a directory called mfront/include/MFront/BehaviourBrick and the second one in a directory called mfront/src subdirectory. Both must be renamed appropriately.

The working directory must now have the following structure:

As in the first part of this document, __Author__, __Date__, __StressCriterionName__ and __STRESS_CRITERION_NAME__ must be replaced by the appropriate values.

2.2 Adding the stress criterion options

In our case, one shall only implement the getOptions method to declare the F and C coefficients.

std::vector<OptionDescription> Green1972StressCriterion::getOptions() const {
  auto opts = StressCriterionBase::getOptions();
  opts.emplace_back("F", "First stress criterion coefficient",
                    OptionDescription::MATERIALPROPERTY);
  opts.emplace_back("C", "Second stress criterion coefficient",
                    OptionDescription::MATERIALPROPERTY);
  return opts;
} // end of Green1972StressCriterion::getOptions()

Note

The default implementation of the isNormalDeviatoric method declares that the normal is not deviatoric, which correct in the case of the Green criterion.

If this is not the case, the implementation of this method must be changed appropriately.

2.3 Compilation of the MFront plugin

Note

This paragraph assumes that you are working under a standard LiNuX environment. In particular, we assume that you use g++ as your C++ compiler. This can easily be changed to match your needs.

The Green1972StressCriterion.cxx can now be compiled in a plugin as follows. Go in the mfront/src directory and type:

$ g++ -I ../include/ `tfel-config --includes `            \
      `tfel-config --oflags --cppflags --compiler-flags`  \
      -DMFRONT_ADITIONNAL_LIBRARY                         \
      `tfel-config --libs` -lTFELMFront                   \
      --shared -fPIC Green1972StressCriterion.cxx         \
      -o libAdditionalStressCriteria.so

The calls to tfel-config allows retrieving the paths to the TFEL headers and libraries. The MFRONT_ADITIONNAL_LIBRARY flag activate a portion of the source file whose only purpose is to register the Green1972 stress criterion in an abstract factory.

#r# Testing the plugin

To test the plugin, go in the tests/test2 directory.

Create a file Green1972PerfectPlasticity.mfront with the following content:

@DSL Implicit;

@Behaviour Green1972PerfectPlasticity;
@Author Thomas Helfer, Jérémy Hure, Mohamed Shokeir;
@Date 25 / 03 / 2020;
@Description {
}

@Algorithm NewtonRaphson;
@Epsilon 1.e-14;
@Theta 1;

@ModellingHypotheses{".+"};
@Brick StandardElastoViscoPlasticity{
  stress_potential : "Hooke" {
    young_modulus : 200e9,
    poisson_ratio : 0.3},
  inelastic_flow : "Plastic" {
    criterion : "Green1972" {
      C : 0.8,
      F : 0.2},
    isotropic_hardening : "Linear" {
      R0 : 150e6}
  }
};

This file can be compiled as follows:

$ MFRONT_ADDITIONAL_LIBRARIES=../../mfront/src/libAdditionalStressCriteria.so \
  mfront -I $(pwd)/../../include/ --obuild --interface=generic                \
  Green1972PerfectPlasticity.mfront

This implementation can be checked with the same MTest file than in the first part of the document.

References

1.
Green, R. J. A plasticity theory for porous solids. International Journal of Mechanical Sciences. 1 April 1972. Vol. 14, no. 4, p. 215–224. DOI 10.1016/0020-7403(72)90063-X. Available from: http://www.sciencedirect.com/science/article/pii/002074037290063X
2.
Fritzen, Felix, Forest, Samuel, Kondo, Djimedo and Böhlke, Thomas. Computational homogenization of porous materials of green type. Computational Mechanics. 1 July 2013. Vol. 52, no. 1, p. 121–134. DOI 10.1007/s00466-012-0801-z. Available from: https://link.springer.com/article/10.1007/s00466-012-0801-z