In this demo, we expand on the stationnary
nonlinear heat transfer demo and consider a transient heat equation
with non-linear heat transfer law including solid/liquid phase change.
This demo corresponds to the TTNL02
elementary test case of the code_aster finite-element
software.
Source files:
- Jupyter notebook: mgis_fenics_heat_equation_phase_change.ipynb
- Python file: mgis_fenics_heat_equation_phase_change.py
- MFront behaviour file: HeatTransferPhaseChange.mfront
The transient heat equation writes:
\[ \rho C_p \dfrac{\partial T}{\partial t} = r-\operatorname{div}\mathbf{j} \]
where \(\rho\) is the material density, \(C_p\) the heat capacity (at constant pressure) per unit of mass, \(r\) represents heat sources and \(\mathbf{j}\) is the heat flux.
In the case of phase changes, the heat capacity exhibits large discontinuities near the transition temperature. It is therefore more suitable to work with the enthalpy density defined as:
\[ h(T) = \int_{T_0}^{T} \rho C_p dT \]
yielding the following heat equation: \[ \dfrac{\partial h}{\partial t} = r-\operatorname{div}\mathbf{j} \]
The thermal material is described by the following non linear Fourier Law:
\[ \mathbf{j}=-k\left(T\right)\,\mathbf{\nabla} T \]
where the thermal conductivity \(k\) is initially assumed to be given by:
\[ k\left(T\right)=\begin{cases} k_s & \text{if }T < T_m \\ k_l & \text{if }T > T_m \end{cases} \] where \(k_s\) (resp. \(k_l\)) denotes the solid (resp. liquid) phase conductivity and \(T_m\) is the solid/liquid transition temperature.
The enthalpy is assumed to be given by:
\[ h\left(T\right)=\begin{cases} c_sT & \text{if }T < T_m \\ c_l(T-T_m)+c_sT_m+\Delta h_{s/l} & \text{if }T > T_m \end{cases} \]
where \(c_s=\rho_sC_{p,s}\) (resp. \(c_l=\rho_lC_{p,l}\)) is the volumic heat capacity of the solid (resp. liquid) phase. It can be observed that the enthalpy exhibits a discontinuity at the phase transition equal to \(\Delta h_{s/l}\) which represents the latent heat of fusion per unit volume.
The enthalpy discontinuity \(\Delta h_{s/l}\) poses convergence difficulties for the Newton resolution. A classical remedy consists in considering a smoothed version of the previous law, such as:
\[ k\left(T\right)=\begin{cases} k_s & \text{if }T < T_s \\ k_s + (k_l-k_s)\dfrac{T-T_s}{T_\text{smooth}} & \text{if } T_s \leq T \leq T_l\\ k_l & \text{if }T > T_l \end{cases} \] and \[ h\left(T\right)=\begin{cases} c_sT & \text{if }T < T_s \\ c_sT_s+\left(\dfrac{cs+cl}{2}+\dfrac{\Delta h_{s/l}}{T_\text{smooth}}\right)(T-T_s) & \text{if } T_s \leq T \leq T_l \\ c_l(T-T_l)+c_sT_s+\dfrac{cs+cl}{2}T_\text{smooth}+\Delta h_{s/l} & \text{if }T > T_l \end{cases} \] where \(T_{smooth}=T_l-T_s\) is a small transition temperature interval between \(T_s=T_m-T_\text{smooth}/2\) the solidus temperature and \(T_l=T_m+T_\text{smooth}/2\) the liquidus temperature.
MFront implementationSimilarly to the stationnary nonlinear
heat transfer demo, the MFront implementation relies on
the DefaultGenericBehaviour DSL and declares the pair of
temperature gradient and heat flux. In addition, the volumic enthalpy
\(h\) is also declared as an internal
state variable. In addition to the two tangent operator blocks
∂j∕∂Δ∇T and ∂j∕∂ΔT already discussed in the
first demo, we also declare the additional block ∂h∕∂ΔT,
referring to the fact that the enthalpy will vary with the temperature
and will enter the transient heat equation.
@DSL DefaultGenericBehaviour;
@Behaviour HeatTransferPhaseChange;
@Author Thomas Helfer / Jérémy Bleyer;
@Date 15 / 02 / 2019;
@Gradient TemperatureGradient ∇T;
∇T.setGlossaryName("TemperatureGradient");
@Flux HeatFlux j;
j.setGlossaryName("HeatFlux");
@StateVariable real h;
h.setEntryName("Enthalpy"); //per unit of volume
@AdditionalTangentOperatorBlock ∂j∕∂ΔT;
@AdditionalTangentOperatorBlock ∂h∕∂ΔT;We now declare the various material properties corresponding to those of aluminium. The material parameters are assumed to be uniform for both phases. Finally, we also introduce the smoothing temperature width \(T_\text{smooth}\).
@Parameter Tₘ = 933.15; // [K]
Tₘ.setEntryName("MeltingTemperature");
@Parameter kₛ = 210; // [W/m/K]
kₛ.setEntryName("SolidConductivity");
@Parameter cₛ = 3.e6; // [J/m^3/K]
cₛ.setEntryName("SolidHeatCapacity");
@Parameter kₗ = 95; // [W/m/K]
kₗ.setEntryName("LiquidConductivity");
@Parameter cₗ = 2.58e6; // [J/m^3/K]
cₗ.setEntryName("LiquidHeatCapacity");
@Parameter Δhₛₗ = 1.08048e9; // [J/m^3]
Δhₛₗ.setEntryName("FusionEnthalpy");
@Parameter Tₛₘₒₒₜₕ = 0.1; // smoothing temperature width [K]
Tₛₘₒₒₜₕ.setEntryName("Tsmooth");We define some local variables corresponding to the values of the conductivity \(k\), the volumic heat capacity \(c\) and the derivative of the heat conductivity with respect to the temperature.
@LocalVariable thermalconductivity k;
@LocalVariable real c;
@LocalVariable real ∂k∕∂T;Again, the behaviour integration is straightforward: after computing
the temperature at the end of the time step T_, we compute
the thermal conductivity, its derivative with respect to the
temperature, the volumic enthalpy and the volumic heat capacity
depending on whether T_ belongs to the solid state (\(T\leq T_s\)), the liquid state (\(T\geq T_l\)) or to the transition region
(\(T_s \leq T \leq T_l\)). We finish by
computing the heat flux.
@Integrator {
const auto T_ = T + ΔT; // current temperature
const auto Tₛ = Tₘ-Tₛₘₒₒₜₕ/2; // solidus temperature
const auto Tₗ = Tₘ+Tₛₘₒₒₜₕ/2; // liquidus temperature
if(T_<Tₛ){ // solid state
k = kₛ;
c = cₛ;
h = cₛ*T_;
∂k∕∂T = 0.;
} else if (T_ > Tₗ) { // liquid state
k = kₗ;
c = cₗ;
h = cₗ*(T_-Tₗ)+Δhₛₗ+cₛ*Tₛ+(cₛ+cₗ)*Tₛₘₒₒₜₕ/2;
∂k∕∂T = 0.;
} else { // solid/liquid smooth transition
k = kₛ + (kₗ-kₛ)*(T_-Tₛ)/Tₛₘₒₒₜₕ;
h = cₛ*Tₛ+((cₛ+cₗ)/2+Δhₛₗ/Tₛₘₒₒₜₕ)*(T_-Tₛ);
c = Δhₛₗ/(Tₗ-Tₛ);
∂k∕∂T = -(kₗ-kₛ)/Tₛₘₒₒₜₕ;
}
// heat flux
j = -k ⋅ (∇T + Δ∇T);
} // end of @IntegratorThe computation of the tangent operator blocks is then straightforward:
@TangentOperator {
∂j∕∂Δ∇T = -k * tmatrix<N, N, real>::Id();
∂j∕∂ΔT = ∂k∕∂T * (∇T + Δ∇T);
∂h∕∂ΔT = c;
} // end of @TangentOperatorWe consider a rectanglar domain of length 0.1 with imposed
temperatures T0 (resp. Ti) on the left (resp.
right) boundaries. We look here for the temperature field T
using a \(P^2\)-interpolation which is
initially at the uniform temperature Ti.
%matplotlib notebook
import matplotlib.pyplot as plt
from dolfin import *
import mgis.fenics as mf
import numpy as np
length = 0.1
width = 0.01
Nx = 1000
Ny = 5
mesh = RectangleMesh(Point(0., 0.), Point(length, width), Nx, Ny, "crossed")
x = np.linspace(0, length, Nx)
V = FunctionSpace(mesh, "CG", 2)
T = Function(V, name="Temperature")
def left(x, on_boundary):
return near(x[0], 0) and on_boundary
def right(x, on_boundary):
return near(x[0], length) and on_boundary
T0 = Constant(853.15)
Ti = Constant(1013.15)
T.interpolate(Ti)
bc = [DirichletBC(V, T0, left),
DirichletBC(V, Ti, right)]We now load the material behaviour
HeatTransferPhaseChange and also change the default value
of Tsmooth to a slightly larger one (but still sufficiently
small). Note that the mesh must be sufficiently refined to use a smaller
value. Indeed, the spatial resolution must be able to capture with a few
elements the sharp transition which will occur during the phase change.
We also verify that 3 different tangent blocks have indeed been defined,
the last one involving the internal state variable Enthalpy
with respect to the temperature.
material = mf.MFrontNonlinearMaterial("./src/libBehaviour.so",
"HeatTransferPhaseChange",
hypothesis="plane_strain",
parameters={"Tsmooth": 1.})
print(["d{}_d{}".format(*t) for t in material.get_tangent_block_names()])['dHeatFlux_dTemperatureGradient', 'dHeatFlux_dTemperature', 'dEnthalpy_dTemperature']The heat equation must also be discretized in time. We use here the \(\theta\)-method and approximate:
\[ \left.\dfrac{\partial h}{\partial t}\right|_{t=t_{n+\theta}} \approx \dfrac{h_{t=t_{n+1}}-h_{t=t_{n}}}{\Delta t} = r_{t=t_{n+\theta}}-\operatorname{div}\mathbf{j}_{t=t_{n+\theta}} \]
where \(\star_{t=t_{n+\theta}}= \theta\star_{t=t_{n+1}}+(1-\theta)\star_{t=t_{n}}\).
The weak formulation therefore reads (in the absence of source terms):
Find \(T\in V\) such that: \[ \int_\Omega \left((h_{t=t_{n+1}}(T)-h_{t=t_{n}})\widehat{T} - \Delta t (\theta\mathbf{j}_{t=t_{n+1}}(T, \nabla T)+(1-\theta)\mathbf{j}_{t=t_{n}})\cdot \nabla \widehat{T} \right)\text{ dx} = 0 \]
in which, at time \(t_{n+1}\), both the enthalpy \(h_{t=t_{n+1}}\) and the heat flux \(\mathbf{j}_{t=t_{n+1}}\) are non-linear functions of the unknown temperature.
We therefore see that the above non-linear problem does not fit into
the default form of a MFrontNonlinearProblem residual. We
will therefore have to specify its form manually. To do so, we need to
get the functions h and j associated to the
current values of the enthalpy and the heat flux.
Second, we must call the initialize method which
initializes the functions associated with gradients, fluxes, external
and internal state variables objects and the corresponding tangent
blocks. All gradients and external state variables must have been
registered before calling this method. In this case, we rely on the
automatic registration of the temperature and its gradient.
Finally, to implement the \(\theta\)
time discretization scheme, we will also need to keep track of the
enthalpy and heat flux values at the previous time step. We can simply
define these new functions as deep copies of h and
j. Doing so, h_old and j_old will
also be Quadrature functions.
problem = mf.MFrontNonlinearProblem(T, material, quadrature_degree=2, bcs=bc)
h = problem.get_state_variable("Enthalpy")
j = problem.get_flux("HeatFlux")
problem.initialize()
j_old = j.copy(deepcopy=True)
h_old = h.copy(deepcopy=True) Automatic registration of 'TemperatureGradient' as grad(Temperature).
Automatic registration of 'Temperature' as an external state variable.We are now ready to define the expression of the above residual. Note
that we must use the integration measure dx associated with
the MFrontNonlinearProblem containing the correct
quadrature degree matching that of the various Quadrature functions.
Finally, the tangent form can be automatically computed using the
compute_tangent_form method from the residual expression
and the structure of the different tangent blocks.
dt = Constant(0.)
theta = Constant(1.)
T_ = TestFunction(V)
j_theta = theta*j + (1-theta)*j_old
problem.residual = (T_*(h - h_old)-dt*dot(grad(T_), j_theta))*problem.dx
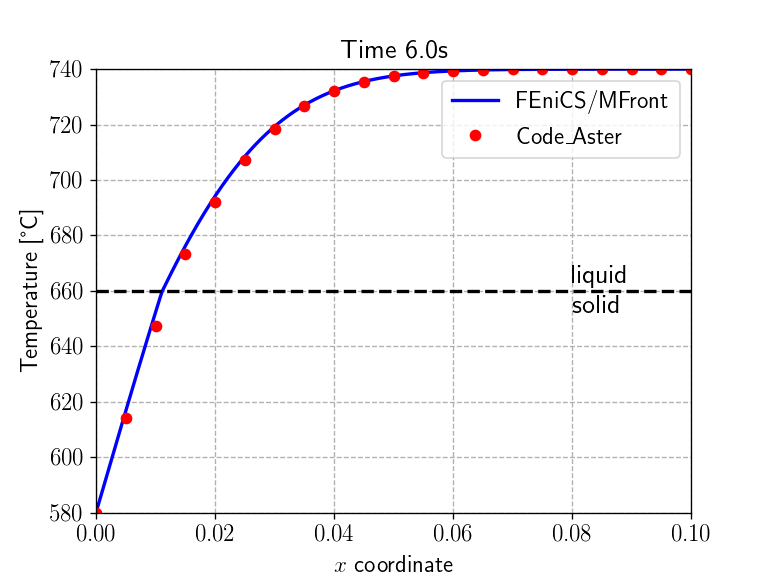
problem.compute_tangent_form()code_aster resultsWe now implement the time-stepping loop which simply solves the
non-linear problem and update the fields corresponding to the values at
the previous time step. We also load the values of the one-dimensional
temperature field \(T(x, t)\) given in
the code_aster test-case and compare them with what we
obtain every second.
cA_results = np.loadtxt("results_code_Aster.csv", delimiter=",")
code_Aster_times = np.arange(1, 7)
Nsteps = 60
times = np.linspace(0, 6., Nsteps+1)
for (t, delta_t) in zip(times[1:], np.diff(times)):
dt.assign(Constant(delta_t))
problem.solve(T.vector())
h_old.assign(h) # update enthalpy
j_old.assign(j) # update heat flux
sol_time = np.isclose(t, code_Aster_times)
if any(sol_time):
plt.figure()
plt.title("Time {:0.1f}s".format(t), fontsize=16)
ax1 = plt.gca()
ax1.set_xlabel('$x$ coordinate')
ax1.set_ylabel('Temperature [°C]')
ax1.plot(x, np.array([T(xi, width/2)-273.15 for xi in x]), "-b", label="FEniCS/MFront")
ax1.plot(cA_results[:, 0], cA_results[:, np.where(sol_time)[0]+1], "or", label="Code\_Aster")
Tm = material.get_parameter("MeltingTemperature") - 273.15
ax1.plot(x, Tm + 0*x, "--k")
ax1.annotate("liquid\nsolid", xy=(0.08, Tm), fontsize=16, va="center")
plt.legend()
plt.show() <IPython.core.display.Javascript object>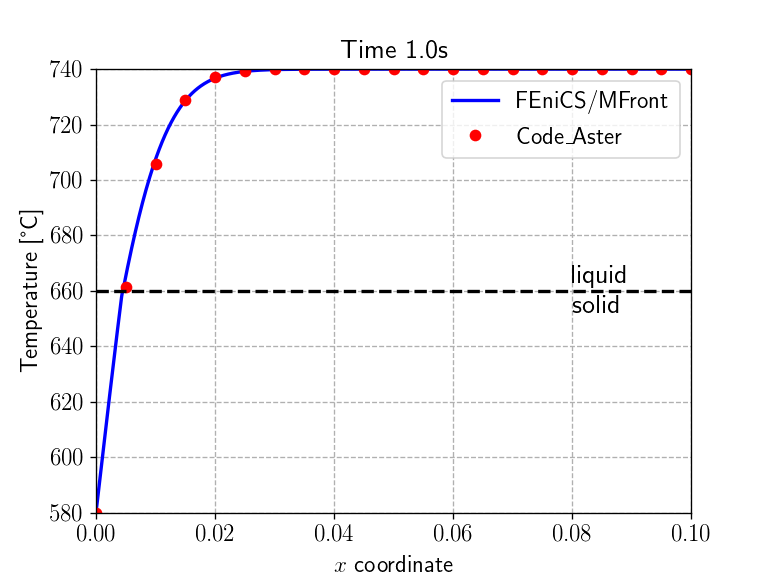
<IPython.core.display.Javascript object>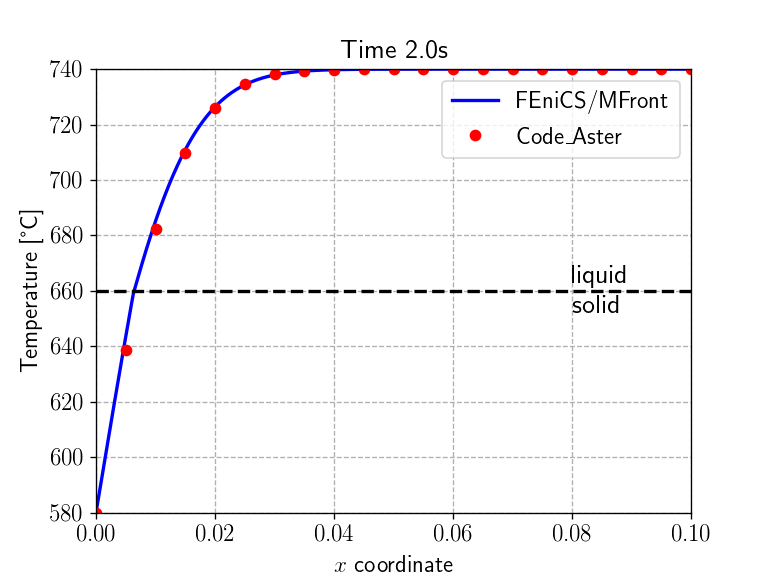
<IPython.core.display.Javascript object>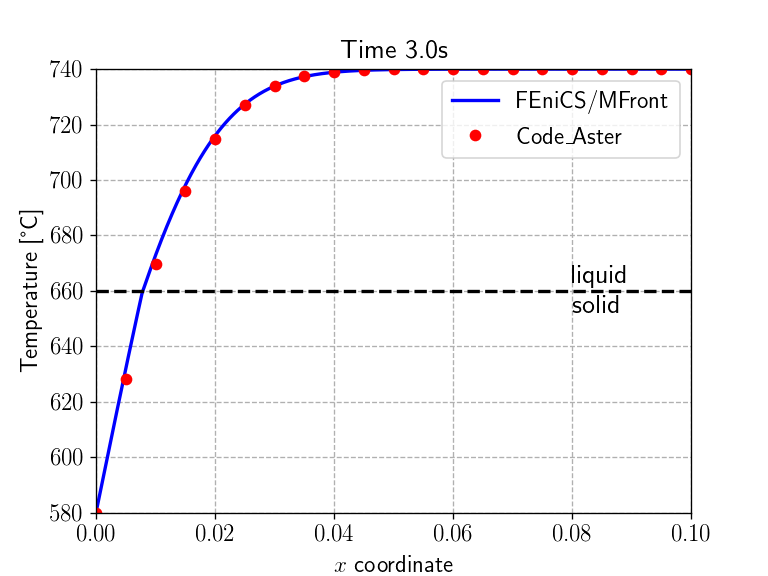
<IPython.core.display.Javascript object>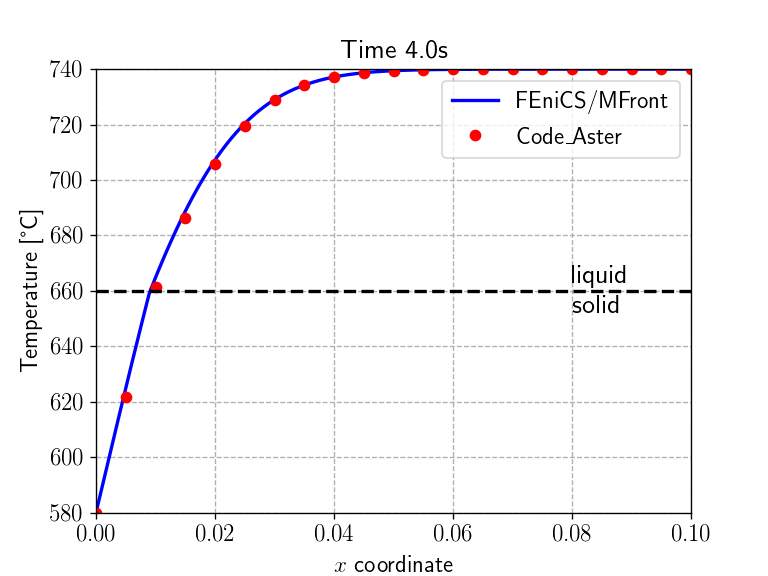
<IPython.core.display.Javascript object>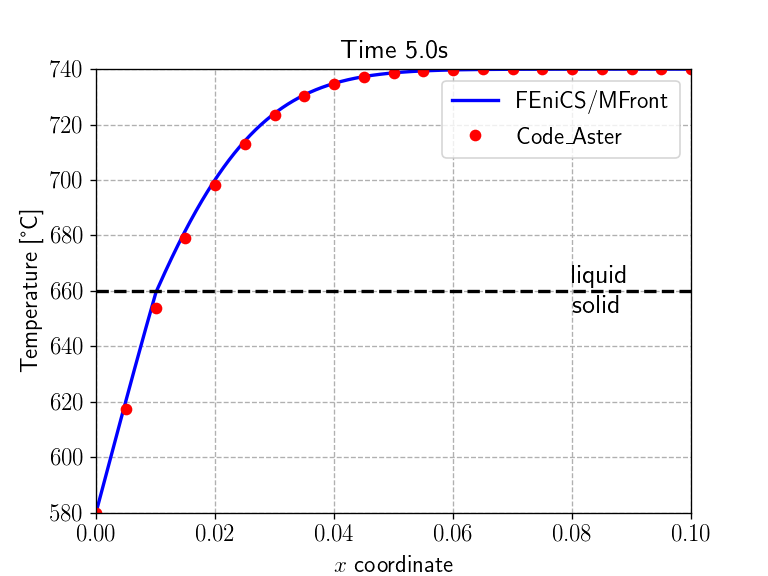
<IPython.core.display.Javascript object>