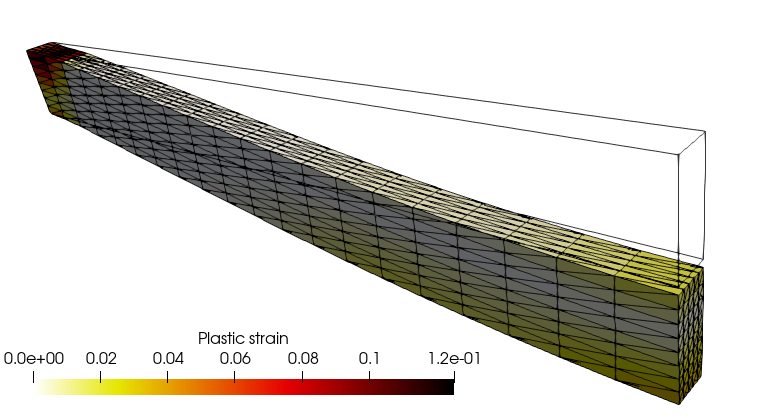
This demo is dedicated to the resolution of a finite-strain elastoplastic problem using the logarithmic strain framework proposed in Miehe, Apel, and Lambrecht (2002).

Source files:

Logarithmic strains

This framework expresses constitutive relations between the Hencky strain measure \(\boldsymbol{H} = \dfrac{1}{2}\log (\boldsymbol{F}^T\cdot\boldsymbol{F})\) and its dual stress measure \(\boldsymbol{T}\). This approach makes it possible to extend classical small strain constitutive relations to a finite-strain setting. In particular, the total (Hencky) strain can be split additively into many contributions (elastic, plastic, thermal, swelling, etc.). Its trace is also linked with the volume change \(J=\exp(\operatorname{tr}(\boldsymbol{H}))\). As a result, the deformation gradient \(\boldsymbol{F}\) is used for expressing the Hencky strain \(\boldsymbol{H}\), a small-strain constitutive law is then written for the \((\boldsymbol{H},\boldsymbol{T})\)-pair and the dual stress \(\boldsymbol{T}\) is then post-processed to an appropriate stress measure such as the Cauchy stress \(\boldsymbol{\sigma}\) or Piola-Kirchhoff stresses.

MFront implementation

The logarithmic strain framework discussed in the previous paragraph consists merely as a pre-processing and a post-processing stages of the behaviour integration. The pre-processing stage compute the logarithmic strain and its increment and the post-processing stage interprets the stress resulting from the behaviour integration as the dual stress \(\boldsymbol{T}\) and convert it to the Cauchy stress.

MFront provides the @StrainMeasure keyword that allows to specify which strain measure is used by the behaviour. When choosing the Hencky strain measure, MFront automatically generates those pre- and post-processing stages, allowing the user to focus on the behaviour integration.

This leads to the following implementation (see the small-strain elastoplasticity example for details about the various implementation available):

@DSL Implicit;

@Behaviour LogarithmicStrainPlasticity;
@Author Thomas Helfer/Jérémy Bleyer;
@Date 07 / 04 / 2020;

@StrainMeasure Hencky;

@Algorithm NewtonRaphson;
@Epsilon 1.e-14;
@Theta 1;

@MaterialProperty stress s0;
s0.setGlossaryName("YieldStress");
@MaterialProperty stress H0;
H0.setEntryName("HardeningSlope");

@Brick StandardElastoViscoPlasticity{
  stress_potential : "Hooke" {
        young_modulus : 210e9,
        poisson_ratio : 0.3
        },
  inelastic_flow : "Plastic" {
    criterion : "Mises",
    isotropic_hardening : "Linear" {H : "H0", R0 : "s0"}
  }
};

FEniCS implementation

We define a box mesh representing half of a beam oriented along the \(x\)-direction. The beam will be fully clamped on its left side and symmetry conditions will be imposed on its right extremity. The loading consists of a uniform self-weight.

%matplotlib notebook
import matplotlib.pyplot as plt
from dolfin import *
import mgis.fenics as mf
import numpy as np
import ufl

length, width, height = 1., 0.04, 0.1
nx, ny, nz = 30, 5, 8
mesh = BoxMesh(Point(0, -width/2, -height/2.), Point(length, width/2, height/2.), nx, ny, nz)

V = VectorFunctionSpace(mesh, "CG", 2)
u = Function(V, name="Displacement")

def left(x, on_boundary):
    return near(x[0], 0) and on_boundary
def right(x, on_boundary):
    return near(x[0], length) and on_boundary

bc = [DirichletBC(V, Constant((0.,)*3), left),
      DirichletBC(V.sub(0), Constant(0.), right)]

selfweight = Expression(("0", "0", "-t*qmax"), t=0., qmax = 50e6, degree=0)

file_results = XDMFFile("results/finite_strain_plasticity.xdmf")
file_results.parameters["flush_output"] = True
file_results.parameters["functions_share_mesh"] = True

The MFrontNonlinearMaterial instance is loaded from the MFront LogarithmicStrainPlasticity behaviour. This behaviour is a finite-strain behaviour (material.is_finite_strain=True) which relies on a kinematic description using the total deformation gradient \(\boldsymbol{F}\). By default, a MFront behaviour always returns the Cauchy stress as the stress measure after integration. However, the stress variable dual to the deformation gradient is the first Piola-Kirchhoff (PK1) stress. An internal option of the MGIS interface is therefore used in the finite-strain context to return the PK1 stress as the “flux” associated to the “gradient” \(\boldsymbol{F}\). Both quantities are non-symmetric tensors, aranged as a 9-dimensional vector in 3D following MFront conventions on tensors.

material = mf.MFrontNonlinearMaterial("./src/libBehaviour.so",
                                      "LogarithmicStrainPlasticity",
                                      material_properties={"YieldStrength": 250e6,
                                                           "HardeningSlope": 1e6})
print(material.behaviour.getBehaviourType())
print(material.behaviour.getKinematic())
print(material.get_gradient_names(), material.get_gradient_sizes())
print(material.get_flux_names(), material.get_flux_sizes())

At this stage, one can retrieve some information about the behaviour:

print(material.behaviour.getBehaviourType())
    StandardFiniteStrainBehaviour
print(material.behaviour.getKinematic())
    F_CAUCHY
print(material.get_gradient_names(), material.get_gradient_sizes())
    ['DeformationGradient'] [9]
print(material.get_flux_names(), material.get_flux_sizes())
    ['FirstPiolaKirchhoffStress'] [9]

The MFrontNonlinearProblem instance must therefore register the deformation gradient as Identity(3)+grad(u). This again done automatically since "DeformationGradient" is a predefined gradient. The following message will be shown upon calling solve:

Automatic registration of 'DeformationGradient' as I + (grad(Displacement)).

The loading is then defined and, as for the small-strain elastoplasticity example, state variables include the ElasticStrain and EquivalentPlasticStrain since the same behaviour is used as in the small-strain case with the only difference that the total strain is now given by the Hencky strain measure.

In particular, the ElasticStrain is still a symmetric tensor (vector of dimension 6). Note that it has not been explicitly defined as a state variable in the MFront behaviour file since this is done automatically when using the IsotropicPlasticMisesFlow domain specific language.

Finally, we setup a few parameters of the Newton non-linear solver.

problem = mf.MFrontNonlinearProblem(u, material, bcs=bc)
problem.set_loading(dot(selfweight, u)*dx)

epsel = problem.get_state_variable("ElasticStrain")

prm = problem.solver.parameters
prm["absolute_tolerance"] = 1e-6
prm["relative_tolerance"] = 1e-6
prm["linear_solver"] = "mumps"

Information about how the elastic strain is stored can be retrieved as follows:

print("'ElasticStrain' shape:", ufl.shape(epsel))
    'ElasticStrain' shape: (6,)

During the load incrementation, we monitor the evolution of the vertical downwards displacement at the middle of the right extremity.

Nincr = 30
load_steps = np.linspace(0., 1., Nincr+1)
results = np.zeros((Nincr+1, 3))
for (i, t) in enumerate(load_steps[1:]):
    selfweight.t = t
    print("Increment ", i+1)
    problem.solve(u.vector())
    p0 = problem.get_state_variable("EquivalentPlasticStrain", project_on=("DG", 0))

    file_results.write(u, t)
    file_results.write(p0, t)
    
    results[i+1, 0] = -u(length, 0, 0)[2]
    results[i+1, 1] = t

This simulation is a bit heavy to run so we suggest running it in parallel:

mpirun -np 4 python3 finite_strain_elastoplasticity.py

The load-displacement curve exhibits a classical elastoplastic behaviour rapidly followed by a stiffening behaviour due to membrane catenary effects.

plt.figure()
plt.plot(results[:, 0], results[:, 1], "-o")
plt.xlabel("Displacement")
plt.ylabel("Load");
<IPython.core.display.Javascript object>

References

Miehe, C., N. Apel, and M. Lambrecht. 2002. “Anisotropic Additive Plasticity in the Logarithmic Strain Space: Modular Kinematic Formulation and Implementation Based on Incremental Minimization Principles for Standard Materials.” Computer Methods in Applied Mechanics and Engineering 191 (47–48): 5383–5425. https://doi.org/10.1016/S0045-7825(02)00438-3.